Model The World

我们来详细探讨香农熵（Shannon entropy）、瑞利熵（Rényi entropy）和塔利斯熵（Tsallis entropy）。这三种熵都是度量概率分布不确定性或信息量的核心工具，但在背景、机制、性质和应用上各有侧重。 核心概念统一性： 它们都基于一个离散随机变量 X，其取值为 {x₁, x₂, ..., xn}，对应的概率分布为 P = (p₁, p₂, ..., pn)，满足 pi ≥ 0 且 Σpi = 1。熵 H(P) 量化了根据该分布抽取一个样本结果的不确定性或信息量。 1. 香农熵 (Shannon Entropy) 背景： 由克劳德·香农于1948年在其开创性论文《通信的数学理论》中提出。 目标是解决可靠和高效通信的基本问题：如何量化消息中包含的“信息”，如何压缩信息（无损压缩的理论极限），以及信道能可靠传输的最大信息速率（信道容量）。 它是信息论的基石。 机制： 定义单个事件 xi 发生的“自信息”为 I(xi) =...

量子态和信道的可区分性、纠缠和信息量可以通过以下方法量化： 1. 量子态和信道的可区分性度量 可区分性度量用于衡量两个量子态或量子信道之间的相似或不同程度。 量子态的可区分性： 迹距离 (Trace Distance)：用于量化两个量子态之间的可区分性。 忠实度 (Fidelity)：衡量两个量子态之间的接近程度。它可以通过半定规划 (Semi-Definite Program, SDP) 计算。根忠实度（Root Fidelity）是联合凹函数。忠实度满足数据处理不等式 (Data-Processing Inequality)，这意味着在量子信道作用下，态之间的忠实度不会降低。 正弦距离 (Sine Distance)：是忠实度的一种变体。 钻石距离 (Diamond Distance)：是另一种用于衡量量子态可区分性的度量。 量子信道的可区分性： 信道忠实度测量 (Fidelity Measures for Channels)：用于衡量量子信道之间的可区分性。 2....

量子信道（Quantum Channels）是描述量子系统与环境相互作用方式的数学对象，它们对量子信息的传输和处理具有深远影响。 量子信道的描述 量子信道通常被定义为将输入量子态映射到输出量子态的线性完全正迹保持（completely positive and trace-preserving, CPTP）映射。它们捕获了量子信息在传输或存储过程中可能经历的所有变化，包括噪声和信息丢失。 有多种数学方式可以表示量子信道： Kraus 算子表示 (Kraus Operators)：一个量子信道 N\mathcal{N}N 可以用一组 Kraus 算子 {Kj}j=1r\{K_j\}_{j=1}^r{Kj​}j=1r​ 来描述，使得对于任何输入状态 XXX，输出为 N(X)=∑j=1rKjXKj†\mathcal{N}(X) = \sum_{j=1}^r K_j X K_j^\daggerN(X)=∑j=1r​Kj​XKj†​。所有 Kraus 算子必须满足 ∑j=1rKj†Kj=I\sum_{j=1}^r K_j^\dagger K_j =...

在量子信息处理中，一系列核心的数学概念和工具构成了理解和分析量子系统行为的基础。这些工具不仅描述了量子态本身，还刻画了量子态如何被测量、如何通过量子信道传输，以及如何量化信息和可区分性。 以下是量子信息处理中一些基本的数学工具及其相互关系： 算子和范数 (Operators and Norms) 算子函数 (Operator Functions)：量子信息论中的许多概念都依赖于对算子执行函数操作。例如，如果 XXX 是一个具有特征分解 X=∑k=1dλk∣ψk⟩⟨ψk∣X = \sum_{k=1}^d \lambda_k |\psi_k\rangle\langle\psi_k|X=∑k=1d​λk​∣ψk​⟩⟨ψk​∣ 的算子，那么 XαX^\alphaXα 的定义取决于 α\alphaα 的值。 对于整数 α∈N\alpha \in \mathbb{N}α∈N， XαX^\alphaXα 的定义为 ∑k=1dλkα∣ψk⟩⟨ψk∣\sum_{k=1}^d \lambda_k^\alpha...

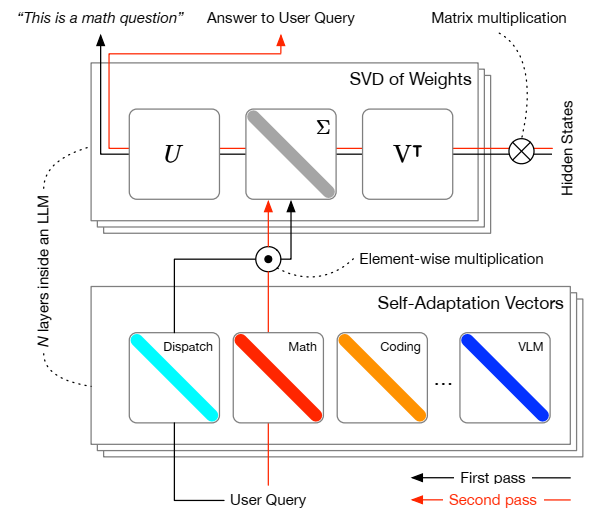
摘要 自适应大型语言模型（LLM）旨在解决传统微调方法带来的挑战，这些方法通常计算密集，处理各种任务的能力是静态的。我们介绍了Transformer2，这是一种新颖的自适应框架，通过选择性地仅调整LLM权重矩阵的奇异分量，实时调整LLM以适应看不见的任务。在推理过程中，Transformer2采用了两步机制：首先，调度系统识别任务属性，然后使用强化学习训练的特定于任务的“专家”向量被动态混合，以获得传入提示的目标行为。我们的方法优于LoRA等无处不在的方法，参数更少，效率更高。Transformer2展示了不同LLM架构和模式的多功能性，包括视觉语言任务。Transformer2代表了一次重大的飞跃，它提供了一种可扩展、高效的解决方案，用于增强LLM的适应性和特定任务的性能，为真正动态、自组织的人工智能系统铺平了道路。代码在 https://github.com/SakanaAI/self-adaptive-llms

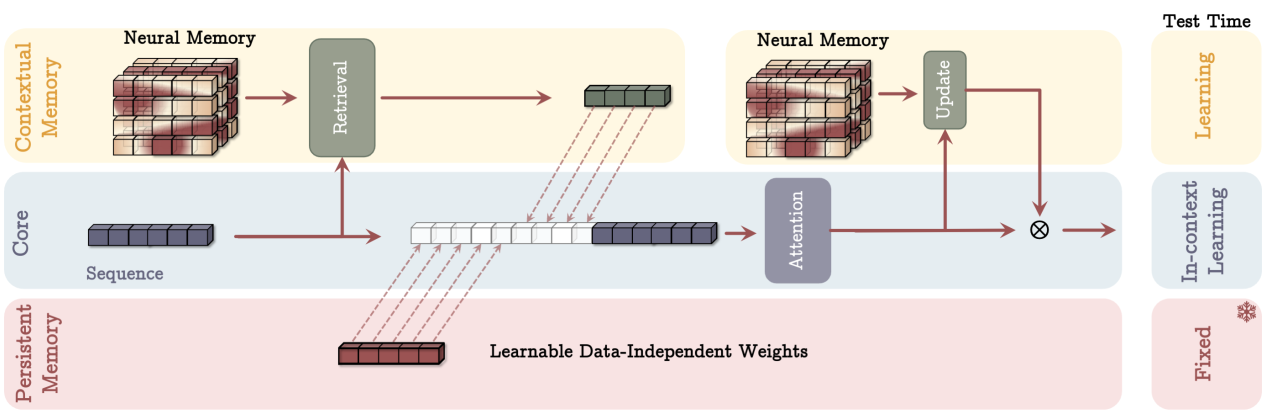
摘要 十多年来，人们对如何有效利用循环模型和注意力进行了广泛的研究。虽然循环模型旨在将数据压缩到固定大小的内存中（称为隐藏状态），但注意力允许关注整个上下文窗口，捕获所有标记的直接依赖关系。然而，这种更精确的依赖关系建模伴随着二次成本，将模型限制在固定长度的上下文中。我们提出了一种新的神经长期记忆模块，可以学习记忆历史背景，并在利用很久以前的信息的同时帮助注意力关注当前的上下文。我们证明，这种神经记忆具有快速并行训练的优点，同时保持了快速推理。从记忆的角度来看，我们认为注意力由于其有限的上下文但精确的依赖性建模而表现为短期记忆，而神经记忆由于其记忆数据的能力而表现为长期、更持久的记忆。基于这两个模块，我们介绍了一个新的架构系列，称为Titans，并提出了三种变体，以解决如何将内存有效地整合到这个架构中。我们在语言建模、常识推理、基因组学和时间序列任务方面的实验结果表明，Titans比Transformer和最近的现代线性递归模型更有效。与基线相比，它们还可以有效地扩展到大于2M的上下文窗口大小，在大海捞针任务中具有更高的精度。论文地址

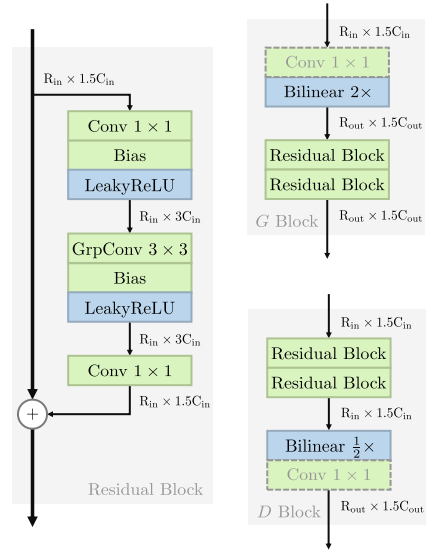
摘要 人们普遍认为GAN难以训练，文献中的GAN架构充斥着经验技巧。我们提供了反对这一说法的证据，并以更有原则的方式建立了一个现代GAN基线。首先，我们推导出了一个行为良好的正则化相对论GAN损失，它解决了之前通过一系列特殊技巧解决的模式下降和不收敛问题。我们从数学上分析了我们的损失，并证明它允许局部收敛保证，这与大多数现有的相对论损失不同。其次，这种损失使我们能够抛弃所有临时技巧，用现代架构替换普通GAN中使用的过时骨干网。以StyleGAN2为例，我们提出了一个简化和现代化的路线图，该路线图产生了一个新的极简主义基线——R3GAN（“Re-GAN”）。尽管简单，但我们的方法在FFHQ、ImageNet、CIFAR和Stacked MNIST数据集上超越了StyleGAN2，并与最先进的GAN和扩散模型进行了比较。 论文地址

...

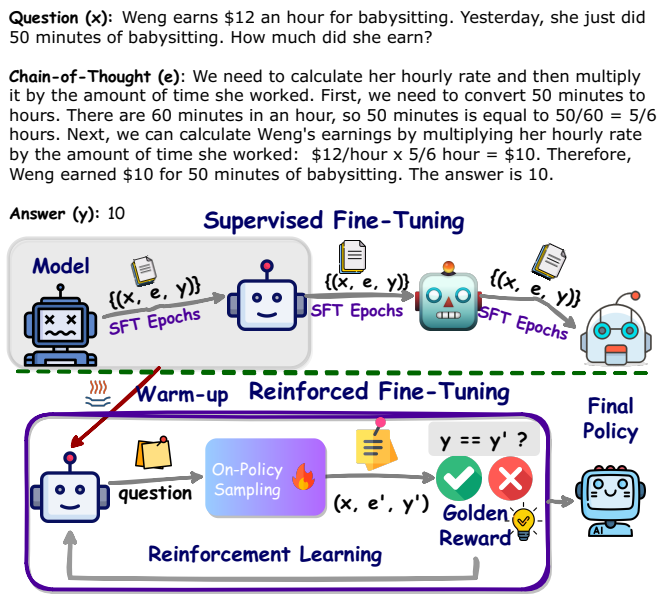
摘要 增强大型语言模型（LLMs）推理能力的一种方式是使用思想连（CoT）注释执行有监督微调（SFT）。然而，该方式不能展示足够强的泛化能力，因为训练仅依赖于给定的CoT数据。在数学问题求解中，例如，在训练数据中每个问题仅有一个注释的推理路径。直观上，算法最好从来自给定问题的多个注释推理路径上学习。为了解决这个问题，我们提出一个简单但有效的方式，称为强化微调（ReFT）来增强学习的LLMs进行推理的泛化能力，使用数学问题求解作为示例。ReFT首先使用SFT预热模型，然后使用在线强化学习，本文中指定为PPO算法，来进一步微调模型，其中，给定问题，会自动采样大量推理路径，并且奖励自然地来自真实答案。在GSM8K、MathQA和SVAMP数据集上进行的广泛实验表明，ReFT的表现明显优于SFT，通过结合多数投票和重新排名等推理时间策略，可以进一步提高性能。请注意，ReFT通过从与SFT相同的训练问题中学习来获得改进，而不依赖于额外的或增强的训练问题。这表明ReFT具有更强的泛化能力。论文地址...