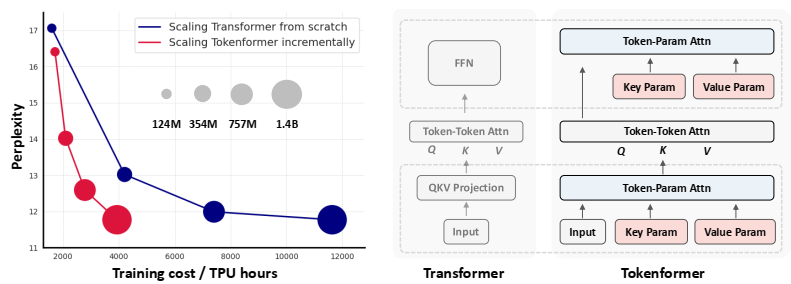
论文阅读十六:SiT:利用可扩展的插值Transformers探索基于流和扩散的生成模型
摘要。 我们提出可扩展插值Transfomrers(SiT),这是建立在扩散Transformers(DiT) 骨干上的一类生成模型。插值框架,比标准扩散模型,允许以一种更为灵活的方式连接两个分布,使得各种影响构建在动态性传输上的生成模型设计选择的模块化研究成为可能:离散或连续时间学习、目标函数、连接分布的插值,和确定性或随机采样。通过仔细引入上述成分,SiT在条件ImageNet 256×256和512×512基准上,使用完全相同的模型结构、参数数量和GFLOP,在模型大小上均匀地超过了DiT。通过探索各种扩散系数(可以与学习分开调整),SiT的FID-50K得分分别为2.06和2.62。代码可在此处获得:https://github.com/willisma/SiT
引言
当代图像生成的成功来自算法进步、模型架构的改进以及神经网络模型和数据缩放的进步。最先进的扩散模型[25,53]通过将数据增量转换为迭代随机过程规定的高斯噪声来进行,该过程可以在离散或连续时间中指定。在抽象层面上,这种破坏过程可以被视为定义了一个时间依赖的分布,该分布从原始数据分布迭代平滑到标准正态分布。扩散模型学习如何逆转这种破坏过程,并沿此连接向后推高斯噪声以获得数据样本。学习执行此转换的对象通常预测损坏过程中的噪声[25]或连接数据和高斯分布的分数[64],尽管存在这些选择的替代方案[28,56]。虽然扩散模型最初用U-Net架构表示这些对象[25,54],但最近的工作强调了视觉架构的进步,如视觉变换器(ViT)[21]可以整合到标准扩散模型管道中以提高性能[50]。
与此相对应的是,大量研究人员致力于探索噪声过程的结构,这已被证明能带来性能上的优势[33,36,37,60]。然而,许多研究并没有超越将数据通过具有均衡分布的扩散过程的概念,这是数据与高斯之间的一种受限类型的连接。最近引入的随机插值法 [2] 解除了这一限制,并在噪声与数据的连接中引入了更多灵活性。在本文中,我们系统地探讨了这种灵活性对大规模图像生成性能的影响。
直观地说,我们认为学习问题的难度可能与所选择的特定连接和所学习的对象有关。我们的目的是澄清这些设计选择,以简化学习问题,从而提高性能。为了了解学习问题中潜在的好处在哪里,我们从去噪扩散概率模型(DDPM)开始,并对以下内容进行调整:(i)学习哪个对象,以及(ii)选择哪个插值来揭示最佳实践。
除了学习问题,还有一个采样问题必须在推理时解决。对于扩散模型,人们已经认识到采样可以是确定性的或随机的[63],采样方法的选择可以在学习过程后进行。然而,用于随机采样的扩散系数通常被表示为与正向噪声过程有内在联系,而通常情况并非如此。
在本文中,我们探讨了插值子的设计以及将结果模型用作确定性或随机性采样器对性能的影响。通过在设计空间中采取一系列正交步骤,我们逐渐从典型的去噪扩散模型过渡到插值模型。随着我们的进展,我们仔细评估了每一次偏离扩散模型对性能的影响。总之,我们的主要贡献是:
– 我们通过四个关键组成部分的组合系统地研究了SiT设计空间:时间离散化、模型预测、插值和采样器。
- 我们为每个组件的选择提供理论动力,并研究它们如何提高实际性能。
- 我们利用了随机采样器扩散系数的可调性,并表明其自适应可以加强对模型和目标之间KL散度的控制。
- 我们展示了这如何在不进行任何额外再训练的情况下带来实证效益。
- 结合每个组件中确定的最佳设计选择,我们的SiT模型在256×256和512×512图像分辨率上都超过了扩散变换器(DiT),分别获得了2.06和2.62的FID-50K分数,而无需修改模型的任何结构或超参数。
SiT:可扩展的插值Transformers
我们首先回顾了构建基于流和基于扩散的生成模型的主要成分。
流和扩散
流和扩散模型都是利用随机过程来渐进将噪声 转为生成任务的数据 。这种时变过程可以概述如下:
其中, 是t的递减函数, 是t的递增函数。随机插值和其他流匹配方法[2,4,41,43]将过程(1)限制在 上,且设置 ,因此 准确地在插值在时间t=0的 和时间t=1的 之间。相反,基于分数的扩散模型[33,37,64]通过前向时间随机微分方程(SDE)间接设置 和 ,其平衡分布为 ,即 收敛到 ,仅当 。
尽管在制定随机过程 时存在细微差别,但随机插值和基于分数的扩散模型的共同点是, 可以使用逆时间SDE或概率流常微分方程(ODE)进行动态采样。
概率流ODE。(1)中 的边际概率分布 与具有速度场的概率流ODE的分布一致:
其中,v(x,t)由条件期望给出:
和(2)与公式(3)之间的对应关系见附录A.1。通过从 逆时间求解(2),我们可以从 生成样本,这近似于真实数据分布p(x)。我们将(2)称为基于流的生成模型。
逆时间SDE。 的时变概率分布 也与逆时间SDE[5]的分布一致:
其中, 是逆时间维纳过程, 是任意时变扩散系数,v(x,t)是(3)中定义的速度, 是分数。类似于v,这个分数由条件期望给出:
同样, 和(4)与公式(5)之间的对应关系在附录A.3中推导出来。从 向后求解逆SDE(4),可以从近似的数据分布 生成样本。我们将(4)称为随机生成模型。
设计选择。基于分数的扩散模型通常将(4)中 、 和 的选择与生成 的正向SDE中使用的漂移和扩散系数联系起来(见下文(10))。随机插值框架将 的公式与正向SDE解耦,并表明在 、 和 的选择上有更大的灵活性。下面,我们将利用这种灵活性来构建生成模型,在图像生成任务中,这些模型在标准基准上优于基于分数的扩散模型。
估算分数和速度
概率流ODE(2)和逆时SDE(4)作为生成模型的实际使用依赖于我们估计输入这些方程的速度v(x,t)和/或分数s(v,t)项的能力。基于分数的扩散模型中的关键观察结果是,分数可以使用损失参数化地估计为 :
这种损失可以通过使用(5)以及条件期望的标准属性来推导。同样,(3)中的速度可以通过损失参数化地估计为
我们注意到,任何与时间相关的权重都可以包含在(6)和(7)中的积分下。当T变大时,这些权重因素在基于分数的模型中是关键[36];相比之下,对于T=1且没有任何偏差的随机插值,这些权重不太重要,可能会带来数值稳定性问题(见附录B)。
模型预测。我们观察到,在实践中只需要估计 和 中的一个。这直接来自约束
其可用于根据速度(3)将分数(5)重新表示为
我们在附录a.4中包含了详细的推导。值得注意的是,给定(9)提出的简单线性关系,我们也可以用s(x,t)表示v(x,t)。我们将使用此关系来指定我们的模型预测。在我们的实验中,我们通常学习速度场v(x,t),并在使用SDE进行采样时用它来表示分数s(x,t)。
请注意,根据我们的定义 和 ,因此(9)的分母永远不会为零。然而, 在t=0时消失,使得(9)中的 导致奇点。这建议在(4)中选择wt=σt来消除这种奇异性,我们将在数值实验中探索其性能。
时间离散化。上述目标函数是在连续时域上定义的,与DDPM不同,DDPM将学习中使用的时间网格与采样中使用的网格耦合在一起。连续时间学习允许我们指定后验采样中使用的离散化,这允许采样效率和性能的灵活性。
指定插值过程
在第2.1节中,我们给出了随机插值和基于分数的扩散的插值(αt和σt)的一般定义。在本节中,我们将深入探讨更多细节,并指定在实验中要探索的三种插值方法。
基于分数的扩散。我们遵循[64]并在正向时间中使用标准方差保持(VP)SDE
结论
在这项工作中,我们提出了可扩展的插值Transformers,这是一个简单而强大的图像生成任务框架。在该框架内,我们探讨了许多关键设计选择之间的权衡:连续或离散时间模型的选择、插值的选择、模型预测的选择和扩散系数的选择。我们强调了每种选择的优缺点,并展示了谨慎的决策如何显著提高性能。许多并行工作[24,32,42,47]在各种下游任务中探索了类似的方法,我们将SiT的应用留给了这些任务,以备将来的工作。