PPDM

在本节中，我们将讨论扩散模型。关于如何推导扩散模型，有许多不同的观点，例如分数匹配、微分方程等。我们将遵循Ho等人关于去噪扩散概率模型的原始论文中概述的方法。

在我们讨论数学细节之前，让我们从VAE扩展的角度总结DDPM：

扩散模型是增量更新，其中整体的组合为我们提供了编码器-解码器结构。

为何增量？这就像改变一艘大船的方向。你需要把船慢慢转向你想要的方向，否则你会失去控制。同样的原则也适用于贵公司的人力资源和大学管理。

Bend one inch at a time.

好了，哲学说得够多了。我们回到正题吧。

DDPM与Sohl Dickstein等人2015年的一项早期工作有很多联系。Sohl-Dickstein等人提出了如何从一种分布转换到另一种分布的问题。VAE提供了一种方式：参考上一节，我们可以认为源分布是潜在变量\(z\sim p(z)\)，目标分布是输入变量\(x\sim p(x)\)。然后，通过设置代理分布\(p_{\theta}(x|z)\)和\(q_{\phi}(z|x)\)，我们可以训练编码器和解码器，使解码器能够实现生成图像的目标。但是VAE在很大程度上是一步生成的：如果你给我们一个潜码z，我们要求神经网络\(f_{\theta}(\cdot)\)立即返回生成的信号\(x\sim N(x|f_{\theta}(z), \sigma_{dec}^2I)\)。从某种意义上说，这对神经网络的要求太高了。我们要求它用几层神经元就能立即将一个分布 p(z) 转换为另一个分布 p(x)。这太过分了。

Sohl-Dickstein等人提出的想法是构建一个转化链，而不是一步过程。为此，他们定义了两个类似于VAE中的编码器和解码器的过程。他们将编码器称为正向过程，将解码器称为反向过程。在这两个过程中，它们都考虑了一系列变量\(x_0,\dots,x_T\)，其正向和反向过程的联合分布分别表示为\(q_{\phi}(x_{0:T})\)和\(p_{\theta}(x_{0:T})\)。为了使这两个过程易于处理（也更灵活），它们采用了马尔可夫链结构（即无记忆），其中

\[\text{正向}\quad x_0\rightarrow x_T: \quad\quad q_{\phi}(x_{0:T}) = q(x_0)\prod_{t=1}^T q_{\phi}(x_t| x_{t-1}),\]

\[\text{反向}\quad x_T\rightarrow x_0: \quad\quad p_{\theta}(x_{0:T}) = p(x_T)\prod_{t=1}^T p_{\theta}(x_{t-1}| x_t).\]

在这两个方程中，过渡分布仅取决于其前一阶段。因此，如果每个转换都是通过某种形式的神经网络实现的，那么整个生成过程就会被分解为许多较小的任务。这并不意味着我们需要多T倍的神经网络。我们只是重复使用一个网络T次。

将整个过程分解为更小的步骤，使我们能够在每个步骤中使用简单的分布。正如以下小节将讨论的那样，我们可以使用高斯分布进行转换。由于高斯的特性，如果似然性和先验性都是高斯的，则后验将保持高斯状态。因此，如果上述每个过渡分布都是高斯分布，则联合分布也是高斯分布。由于高斯函数完全由前两个矩（均值和方差）表征，因此计算非常容易处理。在Sohl-Dickstein等人的原始论文中，也有一个二项式扩散过程的案例研究。

在对概念进行高层次概述之后，我们来讨论一些细节。扩散模型的出发点是考虑 VAE 结构，并将其构建为一个增量更新链，如图 2.1 所示。

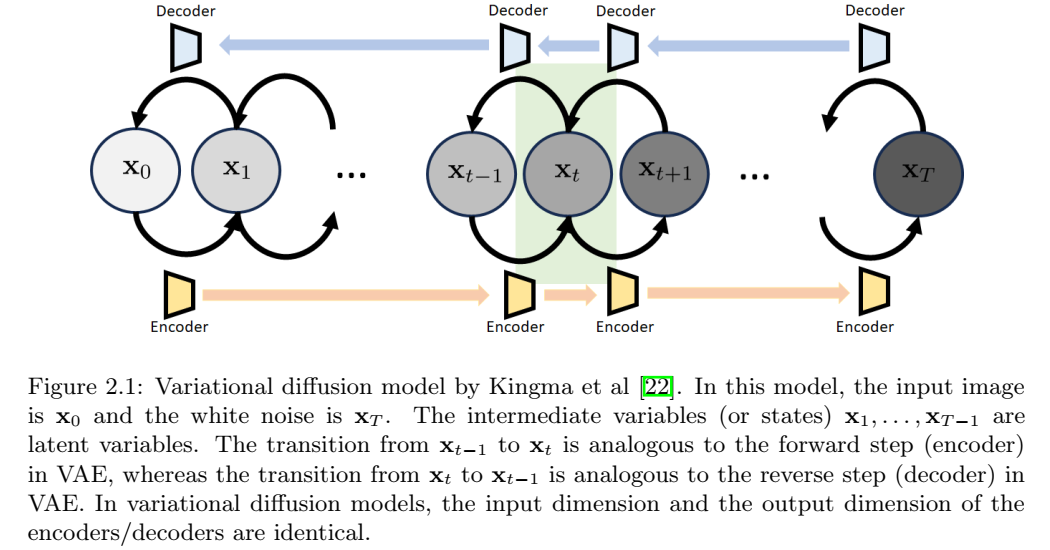
这种特殊的结构被称为变分扩散模型，这是Kingma等人在2021年给出的名字。具有状态序列\(x_0,\dots,x_T\)的变分扩散模型有以下解释：

• \(x_0\): 原始图像，与VAE中的x一样。
• \(x_T\): 潜在变量，与VAE中的z一样。如上所述，为了简单性、可处理性和计算效率，我们选择\(X_t\sim N(0,I)\)。
• \(x_1,\dots,x_{T-1}): 中间状态。也是潜在变量，但不是白高斯。

变分扩散模型的结构由两条路径组成。正向路径和反向路径类似于单步变分自编码器的路径。不同之处在于编码器和解码器具有相同的输入输出维度。所有正向构建块的组合将得到编码器，所有反向构建块的组合将得到解码器。