VAE

我们首先讨论VAE的示意图。如下图所示，VAE由一对模型组成（通常由深度神经网络实现）。位于输入端附近的称为编码器，而位于输出端附近的则称为解码器。我们将输入（通常是图像）表示为向量x，将输出（通常是另一个图像）表示为由向量\(\hat{x}\)。位于编码器和解码器之间中间的向量被称为潜在变量，表示为z。编码器的工作是提取x的有意义的表示，而解码器的工作是从潜在变量z生成新的图像。

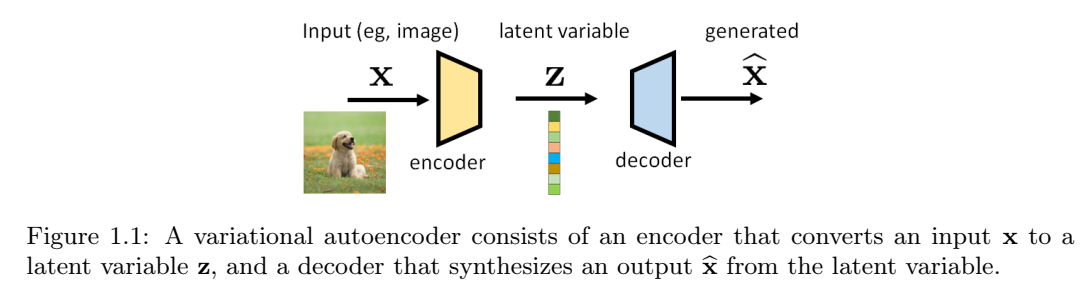
潜在变量z在此设置中有两个特殊作用。对于输入，潜在变量封装了可用于描述x的信息。编码过程可能是一个有损的过程，但我们的目标是尽可能多地保留x的重要内容。关于输出，潜在变量充当可以生成图像\(\hat{x}\)的“种子”。理论上，两个不同的z应该给我们两个不同生成的图像。

下面给出了潜在变量的更正式的定义。

定义 1.1 潜变量。概率模型中，潜变量z是我们没有观测到的变量，且因此不是训练集的一部分，尽管它们是模型的一部分。

示例 1.1 获得图像的潜在表示并不是一件陌生的事情。回到JPEG压缩（它可以说是恐龙）时代，我们使用离散余弦变换（DCT）基函数\(\phi_n\)来编码图像的底层图像/补丁。系数向量\(z=[z_1,\dots,z_N]^T\)是通过将图像x投影到由基函数跨越的空间上，通过\(z_n=\langle\phi_n,x\rangle\)得到的。因此，给定图像x，我们可以产生系数向量z。从z，我们可以使用逆变换来恢复（即解码）图像。

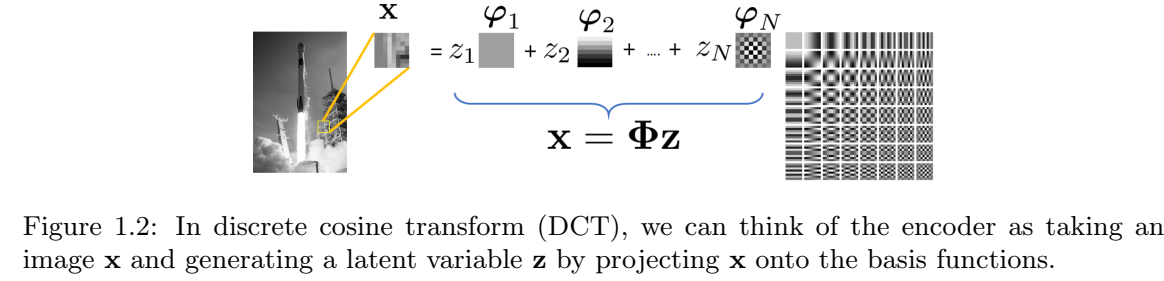
在这个例子中，系数向量z是潜在变量。编码器是DCT变换，解码器是逆DCT变换。

VAE中的“变分”一词与研究函数优化的变分法有关。在VAE中，我们有兴趣寻找描述x和z的最佳概率分布。有鉴于此，我们需要考虑一些分布：

• p（x）：x 的真实分布。它永远无法得知。所有扩散模型都试图找到从 p(x) 中抽取样本的方法。如果我们知道 p(x)（比如说，我们有一个描述 p(x) 的公式），我们就可以抽取一个使 log p(x) 最大化的样本 x。

• p（z）：潜在变量的分布。通常，我们将其设为零均值、单位方差的高斯分布 N(0, I)。原因之一是高斯分布的线性变换仍然是高斯分布，因此这使得数据处理更容易。Doersch也对此进行了很好的解释。文中提到，任何分布都可以通过将高斯分布映射到一个足够复杂的函数来生成。例如，在单变量设置中，逆累积分布函数 (CDF) 技术可用于任何具有可逆 CDF 的连续分布。一般来说，只要我们有一个足够强大的函数（例如神经网络），我们就可以学习它，并将独立同分布的高斯分布映射到我们问题所需的任何潜在变量。

• p(z|x)：与编码器相关的条件分布，它告诉我们给定 x 时 z 的似然值。我们无法获取它。p(z|x) 本身不是编码器，但编码器必须采取一些措施，使其行为与 p(z|x) 保持一致。

• p(x|z)：与解码器相关的条件分布，它告诉我们给定 z 得到 x 的后验概率。同样，我们无法访问它。

当我们从经典参数模型切换到深度神经网络时，潜在变量的概念就变成了深度潜在变量。金玛和韦林给出了一个很好的定义。

定义1.2 深层潜在变量。深层潜在变量是分布p（z）、p（x|z）或p（z|x）由神经网络参数化的潜在变量。

深层潜变量的优点是，即使先验分布和条件分布的结构相对简单（例如高斯分布），它们也可以对非常复杂的数据分布p（x）进行建模。一种思考方式是，神经网络可用于估计高斯分布的均值。虽然高斯本身很简单，但平均值是输入数据的函数，输入数据通过神经网络生成数据相关的平均值。因此，高斯函数的表现力得到了显著提高。

让我们回到上面的四个分布。下面是一个有点琐碎但有教育意义的例子，可以说明这个想法：

示例1.2 考虑根据高斯混合模型分布的随机变量X，其中潜在变量\(z\in {1,\dots,K}\)表示簇恒等式，使得\(p_Z(k) = P[z=K]=\pi_k\)，\(k=1,\dots, K\)。我们假设\(\sum_{k=1}^K\pi_k=1\)。然后，如果我们被告知只需要看第k个簇，则给定Z的X的条件分布为 \[p_{X|Z}(x|k) = N(x|\mu_k,\sigma_k^2 I)\]

x的边际分布可以用全概率定律来求，得到 \[p_X(x) = \sum_{k=1}^K p_{X|Z}(x|k)p_Z(k) = \sum_{k=1}^K\pi_k N(x|\mu_k, \sigma_k^2 I).\tag{1.1}\]

因此，如果我们从\(p_X(x)\)开始，编码器的设计问题是构建一个神奇的编码器，使得对于每个样本\(x\sim p_X(x)\)，潜在码将是\(z\in {1,\dots,K}\)，分布为\(z \sim p_Z(k)\)。

为了说明编码器和解码器是如何工作的，让我们假设均值和方差是已知的并且是固定的。否则，我们需要通过期望最大化（EM）算法来估计均值和方差。这是可行的，但繁琐的方程式会破坏这个插图的教育目的。

编码器：我们如何从 x 得到 z？这很容易，因为在编码器中，我们知道 \(p_X(x)\) 和 \(p_Z(k)\)。假设只有两个类 \(z \in {1,2}\)。实际上，你只是在对样本 x 应该属于哪个类别进行二元决策。有很多方法可以进行二元决策。如果你喜欢最大后验概率决策规则，可以检查

\[P_{Z|X}(1|X) \stackrel{\gt \text{calss 1}}{\lt \text{class 2}}p_{Z|X}(2|X), \]

这将返回一个简单的决定：你给我们x，我们告诉你z∈{1,2}。

解码器：在解码器端，如果我们得到一个潜在码\(z\in{1,\dots,K}\)，那么神奇的解码器只需要向我们返回一个样本x，该样本x来自\(P_{X|Z}(x|k) = N(x|\mu_k, \sigma_k^2 I)\)。不同的 z 将返回 K 个混合分量中的一个。如果我们有足够多的样本，整体分布将遵循高斯混合。

这个例子当然过于简单了，因为现实世界的问题可能比具有已知均值和已知方差的高斯混合模型要困难得多。但我们意识到，如果我们想找到神奇的编码器和解码器，我们必须找到两个条件分布\(p(z|x)\)和\(p(x|z)\)。然而，它们都是高维的。

为了表达更有意义的内容，我们需要引入额外的结构，以便将概念推广到更难的问题。为此，我们考虑以下两个代理分布：

• \(q_{\phi}(z|x)\)：p（z|x）的代理，这也是与编码器相关的分布。\(q_{\phi}(z|x)\)可以是任何有向图模型，并且可以使用深度神经网络进行参数化[24，第2.1节]。例如，我们可以定义

\[(\mu, \sigma^2) = \text{EncoderNetwork}_{\phi}(x), \]

\[q_{\phi}(z|x) = N(z|\mu, \text{diag}(\sigma^2)). \tag{1.2}\]

该模型因其可处理性和计算效率而被广泛使用。

• \(p_{\theta}(x|z)\)：p（x|z）的代理，它也是与解码器相关的分布。与编码器一样，解码器也可以通过深度神经网络进行参数化。例如，我们可以定义 \[f_{\theta}(z) = \text{DecoderNetwork}_{\theta}(z), \]

\[p_{\theta}(x|z) = N(x | f_{\theta}(z), \sigma_{dec}^2 I), \tag{1.3} \]

其中，\(\sigma_{dec}\)是一个可以预先确定或可以学习的超参数。

图1.3总结了输入x和潜在z之间的关系以及条件分布。有两个节点x和z。“正向”关系由p（z|x）指定（近似为\(q_{\phi}(z|x)\)），而“反向”关系由p（x|z）指定（并近似为\(p_{\theta}(x|z)\)）。

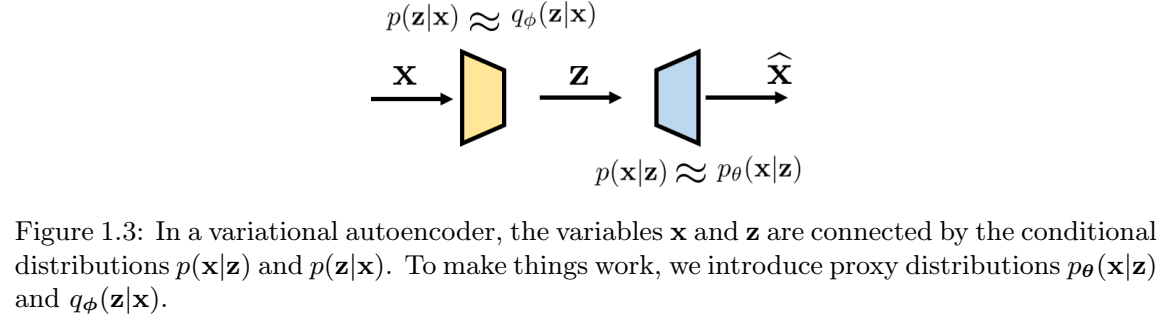
示例 1.3 假设我们有一个随机变量 \(x \in R^d\) 和一个潜在变量 \(z \in R^d\)，使得

\[x \sim p(x) = N(x|\mu, \sigma^2 I),\]

\[z \sim p(z) = N(z | 0, I).\]

我们希望构建一个VAE。通过这种方式，我们的意思是我们想构建两个映射：\(\text{Encoder}(\cdot)\)和\(\text{Decoder}(\cdot)\)。编码器将获取样本x并将其映射到潜在变量z，而解码器将获取潜在变量z并将其对应到生成的变量\(\hat{x}\)。如果我们知道p（x）是什么，那么存在一个简单的解，其中\(z = (x-\mu)/\sigma\),以及\(\hat{x} = \mu + \sigma z\)。在这种情况下，可以确定真实分布，并用δ函数表示：

\[p(x|z) = \delta(x - (\sigma z + \mu)),\]

\[p(z|x) = \delta(z - (x - \mu)/sigma). \]

假设，现在我们不知道p(x)，所以我们需要构建一个编码器和一个解码器来估计z和\(\hat{x}\)。首先定义编码器。在此示例中，我们的编码器接收输入x，并生成参数对\(\hat{\mu}(x)\)和\(\hat{\sigma}(x)^2\)，代表高斯的参数。然后，我们定义\(q_{\phi}(z|x)\)为高斯：

\[(\hat{\mu}(x), \hat{\sigma}^2) = \text{Encoder}_{\phi}(x), \]

\[q_{\phi}(z|x) = N(z|\hat{\mu}(x), \hat{\sigma}(x)^2 I).\]

出于讨论的目的，我们假设\(\hat{\mu}\)是x的仿射函数，使得对于某些参数a和b，\(\hat{\mu}(x) = ax +b \)。类似的，我们假设，对于某些标量t，\(\hat{\sigma}(x)^2 = t^2\)。得到

\[q_{\phi}(z|x) = N(z| ax + b, t^2 I).\]

对于解码器，我们通过考虑以下因素来部署类似的结构

\[(\tilde{\mu}(z), \tilde{\sigma}(z)^2) = \text{Decoder}_{\theta}(z), \]

\[p_{\theta}(x|z) = N(x| \tilde{\mu}(z), \tilde{\sigma}(z)^2 I).\]

同样，为了讨论的目的，我们假设\(\tilde{\mu}\)是仿射的，因此对于某些参数c和v，\(\tilde{\mu}(z) = cz + v\)，对于某些标量s，\(\tilde{\sigma}(z)^2 = s^2\)。因此，\(p_{\theta}(x|z)\)的形式为： \[p_{\theta}(x|z) = N(z| cx + v, s^2 I).\]

我们稍后将讨论如何确定参数。