VAE优化

在前两小节中，我们介绍了VAE和ELBO的构建块。本小节的目的是讨论如何训练VAE以及如何进行推理。

VAE 是一种旨在逼近真实分布 p(x) 以便我们抽取样本的模型。VAE由\((\phi,\theta)\) 参数化。因此，训练 VAE 等同于求解一个优化问题，该问题不仅包含了 p(x) 的本质，而且易于处理。然而，由于 p(x) 难以获取，因此自然而然的替代方案是优化 ELBO，即 log p(x) 的下界。这意味着，VAE 的学习目标是解决以下问题。

定义 1.4 \(\color{blue}{\text{VAE的优化目标是最大化ELBO}}\)： \[(\phi,\theta) = \stackrel{\Large argmax}{\phi,\theta}\sum_{x\in \mathcal{X}}ELBO(x), \tag{1.12}\]

其中，\(\mathcal{X} = \{l=1,\dots,L\}\)是训练数据集。

ELBO梯度的不稳定性。上述优化的挑战在于，ELBO 关于\((\phi,\theta)\) 的梯度难以求解。由于当今大多数神经网络优化器都使用一阶方法，并通过梯度反向传播来更新网络权重，因此难以求解的梯度会给 VAE 的训练带来困难。

让我们详细说明一下梯度的难处理性。我们首先将定义1.3代入上述目标函数。ELBO的梯度为：

\begin{align} \nabla_{\theta,\phi}ELBO(x) &= \nabla_{\theta,\phi}\Big\{E_{q_{\phi}(z|x)}\Bigg[log\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}\Bigg]\Big\}\\ &= \nabla_{\theta,\phi}\Big\{E_{q_{\phi}(z|x)}\Bigg[log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)\Bigg]\Big\}. \tag{1.13} \end{align}

梯度包含两个参数。先来看θ。可以证明 \begin{align} \nabla_{\theta}\ ELBO(x) &= \nabla_{\theta}\Big\{E_{q_{\phi}(z|x)}\Big[log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)\Big]\Big\}\\ &= \nabla_{\theta}\Big\{\int\Big[log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)\Big]\ \cdot\ q_{\phi}(z|x)dz\Big\} \quad\quad\quad&(期望转积分) \\ &= \int\nabla_{\theta}\big\{log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)\big\}\ \cdot\ q_{\phi}(z|x)\ dz &(莱布尼茨法则)\\ &= E_{q_{\phi}(z|x)}\Bigg[\nabla_{\theta}\Big\{log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)\Big\}\Bigg] &(积分转期望)\\ &= E_{q_{\phi}(z|x)}\Bigg[\nabla_{\theta}\Big\{log\ p_{\theta}(x,z)\Big\}\Bigg] &(消除梯度无关项)\\ &\approx \frac{1}{L}\sum_{l=1}^L\nabla_{\theta}\Big\{log\ p_{\theta}(x, z^{(l)})\Big\}, &(蒙特卡洛近似，其中，z^{(l)}\sim q_{\phi}(z|x)) \tag{1.14} \end{align}

其中最后一个等式是期望的蒙特卡罗近似。

在上述方程中，如果\(p_{\theta}(x,z)\)由神经网络等可计算模型实现，则其梯度\(\nabla_{\theta}\{log\ p_{\theta}(x,z)\}\)可以通过自动微分计算出来。因此，可以通过反向传播梯度来实现最大化。

关于\(\phi\)的梯度更加困难。我们可以证明

\begin{align} \nabla_{\phi}\ ELBO(x) &= \nabla_{\phi}\Big\{E_{q_{\phi}(z|x)}\Big[log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)\Big]\Big\}\\ &= \nabla_{\phi}\Big\{\int\Big[log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)\Big]\ \cdot\ q_{\phi}(z|x)dz\Big\} \quad\quad\quad &(期望转积分)\\ &= \int \nabla_{\phi}\big\{\big[log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)\big]\ \cdot\ q_{\phi}(z|x)\big\}\ dz &(莱布尼茨法则，梯度项与\theta求导不同)\\ &\ne \int \nabla_{\phi}\big\{log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)\big\}\ \cdot\ q_{\phi}(z|x)\ dz \\ &= \int \big\{\nabla_{\phi}[log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)]\ \cdot\ q_{\phi}(z|x) + [log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)] \ \cdot\ \nabla_{\phi}q_{\phi}(z|x) \big\} \ dz &(乘法求导公式)\\ &= \int\big[-\nabla_{\theta}log\ q_{\phi}(z|x)\big]\ \cdot\ q_{\phi}(z|x)\ dz + \int\big[ [log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x)]\ \cdot\ q_{\phi}(z|x)\ \cdot\ \nabla_{\theta}log\ q_{\phi}(z|x)\ dz\big]\\ &&(消除梯度无关项，利用对数求导公式，积分拆分)\\ &= E_{q_{\phi}(z|x)}\big[-\nabla_{\phi}log\ q_{\phi}(z|x)\big] + \overbrace{E_{q_{\phi}(z|x)}\big[(log\ p_{\theta}(x,z) - log\ q_{\phi}(z|x))\ \cdot\ \nabla_{\phi}log\ q_{\phi}(z|x)\big]}^{\text{得分函数估计器}}&(积分转期望)\\ &= E_{q_{\phi}(z|x)}\big[\nabla_{\phi}\big\{ - log\ q_{\phi}(z|x)\big\}\big] &(忽略得分函数估计器)\\ &= \frac{1}{L}\sum_{l=1}^L\nabla_{\phi}\big\{-log\ q_{\phi}(z^{(l)}|x)\big\}, &(其中， z^{(l)}\sim q_{\phi}(z|x)). \tag{1.15} \end{align}

正如我们所看到的，即使我们希望保持与θ类似的结构，上述推导中的期望和梯度算子也不能切换。这禁止我们对梯度进行任何反向传播以最大化ELBO。

再参数化技巧。 ELBO梯度的难解性源于这样一个事实，即我们需要从分布\(q_{\phi}(z|x)\)中提取样本z，而分布\(q_{\phi}(z|x)\)本身是\(\phi\)的函数。正如Kingma和Welling所指出的那样，对于连续潜变量，可以计算\(\nabla_{\theta,\phi}\ ELBO(x)\)的无偏估计，这样我们就可以近似计算梯度，从而最大化ELBO。这个想法是采用一种称为重新参数化技巧的技术。

回想一下，潜在变量 z 是从分布\(q_{\phi}(z|x)\)中抽取的样本。重参数化技巧的思路是将 z 表示为另一个随机变量\(\epsilon\) 的可微可逆变换，其分布与 x 和 \(\phi\)无关。也就是说，我们定义一个可微可逆函数 g，使得 \[z = g(\epsilon,\phi,x), \tag{1.16}\]

对于某些随机变量\(\epsilon \sim p(\epsilon)\)。为了简化讨论，我们提出了一个额外的要求，即 \[q_{\phi}(z|x)\ \cdot\ \big|det(\frac{\partial z}{\partial \epsilon})\big| = p(\epsilon),\tag{1.17}\]

其中，\(\frac{\partial z}{\partial \epsilon}\)是Jacobian(雅可比)，\(det(\cdot)\)是矩阵行列式。这一要求与多元微积分中变量的变化有关。下面的例子会说明这一点。

示例 1.7 假设 \(z \sim q_{\phi}(z|x)\stackrel{def}{=}N(z|\mu, diag(\sigma^2))\)。我们可以定义

\[z = g(\epsilon,\phi,x)\stackrel{def}{=}\epsilon\odot\sigma + \mu,\tag{1.18}\]

其中，\(\epsilon\sim N(0,I)\)，“\(\odot\)”表示逐元素乘积。参数\(\phi\)为 \(\phi=(\mu,\sigma^2)\)。对于这种分布的选择，我们可以通过让\(\epsilon=\frac{z-\mu}{\sigma}\)来证明: \begin{align} q_{\phi}(z|x)\ \cdot\ \big|det(\frac{\partial z}{\partial \epsilon})\big| &= \prod_{i=1}^d\frac{1}{\sqrt{2\pi\sigma^2}}exp\big\{-\frac{(z_i-\mu_i)^2}{2\sigma_i^2}\big\}\ \cdot\ \prod_{i=1}^d\sigma_i\\ &= \frac{1}{(\sqrt{2\pi})^d}exp\big\{-\frac{||\epsilon||^2}{2}\big\} = N(0,I) = p(\epsilon). \end{align}

通过以ϵ表示z的重新参数化，我们可以查看一些一般函数\(f(z)\)的 \(\nabla_{\phi}E_{q_{\phi}(z|x)}[f(z)]\)。(稍后，我们将考虑\(f(z) = -log\ q_{\phi}(z|x).\))。为了符号简单起见，我们将\(g(\epsilon,\phi,x)\)写为\(g(\epsilon)\)，尽管我们知道g有三个输入。通过变量的变化，我们可以证明

\begin{align} E_{q_{\phi}(z|x)}\big[f(z)\big] &= \int\ f(z)\ \cdot\ q_{\phi}(z|x)\ dz \\ &= \int\ f(g(\epsilon))\ \cdot\ q_{\phi}(g(\epsilon)|x)\ dg(\epsilon), \quad\quad\quad\quad\quad\quad &(z=g(\epsilon))\\ &= \int\ f(g(\epsilon))\ \cdot\ q_{\phi}(g(\epsilon)|x)\ \cdot\ \big|det(\frac{\partial g(\epsilon)}{\partial \epsilon})\big|\ d\epsilon \\ &&(变量变化导致的雅可比矩阵)\\ &= \int\ f(z)\ \cdot\ p(\epsilon)\ d\epsilon &(方程（1.17)\\ &= E_{p(\epsilon)}[f(z)].\tag{1.19} \end{align}

所以，如果我们想取关于ϕ的梯度，我们可以证明 \begin{align} \nabla_{\phi}E_{q_{\phi}(z|x)}\big[f(z)\big] = \nabla_{\phi}E_{p(\epsilon)}\big[f(z)\big] &= \nabla_{\phi}\Big\{\int f(z)\cdot p(\epsilon)\ d\epsilon\Big\}\\ &=\int\ \nabla_{\phi}\{f(z)\ \cdot\ p(\epsilon)\}\ d\epsilon\\ &=\int\ \{\nabla_{\phi}f(z)\}\cdot p(\epsilon)\ d\epsilon\\ &= E_{p(\epsilon)}[\nabla_{\phi}f(z)], \tag{1.20} \end{align}

这可以用蒙特卡洛近似。代入 \(f(z) = -log\ q_{\phi}(z|x)\)，我们可以证明 \begin{align} \nabla_{\phi}E_{q_{\phi}(z|x)}\big[-log\ q_{\phi}(z|x)\big] &= E_{p(\epsilon)}\big[-\nabla_{\phi}log\ q_{\phi}(z|x)\big]\\ &\approx -\frac{1}{L}\sum_{l=1}^L\nabla_{\phi}log\ q_{\phi}(z^{(l)}|x), \quad\quad\quad&(其中，z^{(l)}= g(\epsilon^{(l)}, \phi, x))\\ &= -\frac{1}{L}\sum_{l=1}^L\nabla_{\phi}\Big[log\ p(\epsilon^{(l)}) - log\big|\text{det}\frac{\partial z^{(l)}}{\partial \epsilon^{(l)}}\big|\Big]\\ &= \frac{1}{L}\sum_{l=1}^L\nabla_{\phi}\Big[log\big|\text{det}\frac{\partial z^{(l)}}{\partial \epsilon^{(l)}}\big|\Big]. \end{align}

因此，只要行列式相对于ϕ可微，蒙特卡洛近似就可以进行数值计算。

示例 1.8 假设参数和分布\(q_{\phi}\)定义如下： \[(\mu,\sigma^2) = \text{EncoderNetwork}_{\phi}(x)\]

\[q_{\phi}(z|x) = N(z|\mu, diag(\sigma^2)).\]

我们可以定义 \(z = \mu + \sigma \odot \epsilon\)，\(epsilon\sim N(0,I)\)。那么，我们可以证明

\begin{align} log\Big|\text{det}\frac{\partial z}{\partial \epsilon}\Big| &= log\Big|\text{det}\Big(\frac{\partial(\mu+\sigma\odot\epsilon)}{\partial \epsilon}\Big)\Big|\\ &= log\ \big|\text{det}(diag\{\sigma\})\big|\\ &= log\prod_{i=1}^d\sigma_i = \sum_{i=1}^d log\sigma_i. \end{align}

因此，我们可以证明 \begin{align} \nabla_{\phi}E_{q_{\phi}(z|x)}[-log\ q_{\phi}(z|x)] &\approx\frac{1}{L}\sum_{l=1}^L\nabla_{\phi}\Big[log\ \Big|\text{det}\ \frac{\partial z^{(l)}}{\partial \epsilon^{(l)}}\Big|\Big]\\ &= \frac{1}{L}\sum_{l=1}^L\nabla_{\phi}\Big[\sum_{i=1}^d log\sigma_i\Big]\\ &= \nabla_{\phi}\Big[\sum_{i=1}^d log\sigma_i\Big]\\ &= \frac{1}{\sigma}\odot \nabla_{\phi}\{\sigma_{\phi}(x)\}, \end{align}

其中我们强调\(\sigma_{\phi}(x)\)是编码器的输出，编码器是一个神经网络。

正如我们在上面的例子中看到的，对于分布的一些特定选择（例如高斯分布），ELBO的梯度可以更容易地推导出来。

VAE编码器。在讨论了重新参数化技巧之后，我们现在可以讨论VAE中编码器的具体结构。为了使我们的讨论更加集中，我们假设编码器的选择相对常见：

\[(\mu,\sigma^2) = \text{EncoderNetwork}_{\phi}(x)\]

\[q_{\phi}(z|x) = N(z|\mu, \sigma^2 I).\]

参数\(\mu\)和\(\sigma\)在技术上是神经网络，因为它们是\(\text{EncoderNetwork}_{\phi}(\cdot)\)的输出。因此，如果我们将它们表示为

\[\mu = \underbrace{\mu_{\phi}}_{\text{neural network}} (x),\]

\[\sigma^2 = \underbrace{\sigma_{\phi}^2}_{\text{neural network}}(x), \]

我们的符号稍微复杂一点，因为我们想强调\(\mu\)是x的函数。您给我们一个图像X，我们的工作是将高斯的参数（即平均值和方差）返回。如果您给我们一个不同的x，那么高斯的参数也应不同。参数\(\phi\)明确指出\(\mu\)由\(\phi\)控制（或参数化）。

假设，给定第\(l\)个训练样本\(x^{(l)}\)。我们想要据此样本生成潜在变量\(z^{(l)}\)，，它是\(q_{\phi}(z|x)\)的样本。由于高斯结构，这相当于说

\[z^{(l)} \sim N(z\ |\ \mu_{\phi}(x^{(l)}), \sigma_{\phi}^2(x^{(l)})I).\tag{1.21}\]

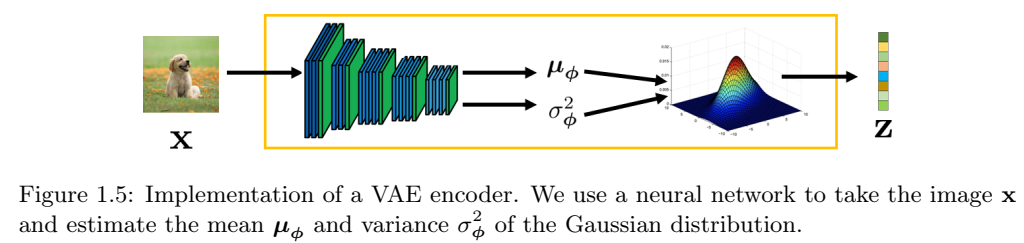
这个方程的有趣之处在于，我们使用\(\text{EncoderNetwork}_{\phi}(\cdot)\)来估计高斯分布的均值和方差。然后，从这个高斯分布中我们得到一个样本\(z^{(l)}\)，如图1.5所示。

表示方程（1.21）的一种更方便的方法是意识到可以使用重新参数化技巧完成采样操作\(z\sim N(\mu,\sigma^2I)\)。

高维高斯的再参数化技巧： \[z\sim N(\mu,\sigma^2I) \Leftrightarrow z= \mu + \sigma\epsilon, \epsilon\sim N(0,I).\tag{1.22}\]

使用再参数化技巧，方差（1.21）可以写为 \[z^{(l)} = \mu_{\phi}(x^{(l)}) + \sigma_{\phi}(x^{(l)})\epsilon, \epsilon\sim N(0,I).\]

证明 我们将证明一个任意协方差矩阵\(\Sigma\)的一般情况,而不是对角矩阵\(\sigma^2 I\)。

对任意高纬高斯\(z\sim N(z|\mu,\Sigma)\)，采样过程可以通过白噪声变换来完成 \[z = \mu + \Sigma^{\frac{1}{2}}\epsilon,\tag{1.23}\]

其中，\(\epsilon\sim N(0,I)\)。半矩阵\(\Sigma^{\frac{1}{2}}\)可以通过特征分解或cholesky分解获得。若\(Sigma\)具有特征分解\(\Sigma=USU^T\)，那么\(\Sigma^{\frac{1}{2}} = US^{\frac{1}{2}}U^T)。特征值矩阵S的平方根是明确的，因为\(Sigma\)是一个半正定矩阵。

我们可以计算z的期望和协方差：

\[E[z] = E[\mu + \Sigma^{\frac{1}{2}}\epsilon] = \mu + \Sigma^{\frac{1}{2}}\underbrace{E[\epsilon]}_{=0} = \mu,\]

\[\text{Cov}(z) = E[(z - \mu)(z-\mu)^T] = E[\Sigma^{\frac{1}{2}}\epsilon\epsilon^T(\Sigma^{\frac{1}{2}})^T] = \Sigma^{\frac{1}{2}}\underbrace{E[\epsilon\epsilon^T]}_{=I}(\Sigma^{\frac{1}{2}})^T = \Sigma.\]

因此，对于对角矩阵\(\Sigma = \sigma^2I\)，上述可简化为 \[z = \mu + \sigma\epsilon, \quad\quad \text{where}\ \epsilon\sim N(0,I).\tag{1.24}\]

给定VAE编码器结构和\(q_{\phi}(z|x)\)，我们可以回到ELBO。回想一下，ELBO由先验匹配项和重建项组成。先验匹配项根据KL散度\(D_{KL}(q_{\phi}(z|x)||p(z))\)进行测量。让我们来评估KL散度。

为了评估KL散度，我们（重新）使用我们总结如下的结果：

定理 1.3 两个高斯的KL散度。 两个d维高斯\(N(\mu_0,\Sigma_0)\)和\(N(\mu_1,\Sigma_1)\)的KL散度为 \begin{align}D_{KL}(N(\mu_0, \Sigma_0)\ ||\ N(\mu_1,\Sigma_1)) \\ = \frac{1}{2}(Tr(\Sigma_1^{-1}\Sigma_0) - d + (\mu_1 - \mu_0)^T\Sigma_1^{-1}(\mu_1-\mu_0) + log\ \frac{\text{det}\Sigma_1}{\text{det}\Sigma_0}). \tag{1.25}\end{align}

通过考虑以下因素来替换我们的分布 \[\mu_0 = \mu_{\phi(x)}, \quad\quad\Sigma_0 = \sigma_{\phi}^2(x)I\]

\[\mu_1 = 0, \quad\quad\quad \Sigma_1=I,\]

我们可以证明KL散度有一个解析表达式

\[D_{KL}(q_{\phi}(z|x)\ ||\ p(z)) = \frac{1}{2}(\sigma_{\phi}^2(x)d - d + ||\mu_{\phi}(x)||^2 - 2dlog\ \sigma_{\phi}(x)), \tag{1.26}\]

其中，d是向量z的维度。KL散度关于\(\phi\)的梯度没有闭合形式，但可以通过数值计算得出：

\[\nabla_{\phi}D_{KL}(q_{\phi}(z|x)\ ||\ p(z)) = \frac{1}{2}\nabla_{\phi}(\sigma_{\phi}^2(x)d - d + ||\mu_{\phi}(x)||^2 - 2dlog\ \sigma_{\phi}(x)).\tag{1.27}\]

相对于θ的梯度为零，因为各项均不依赖于θ。

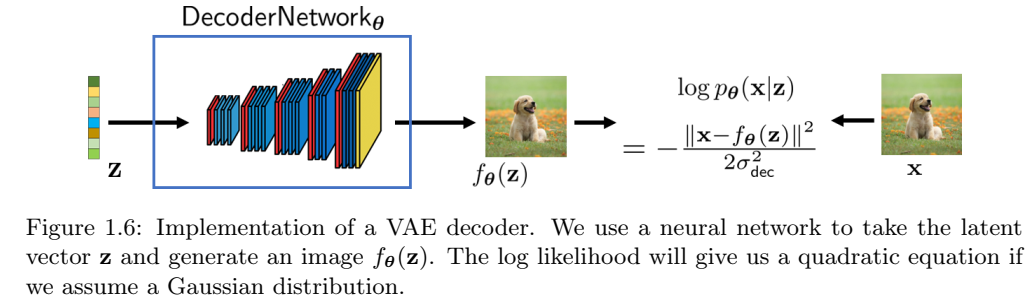
VAE解码器。 解码器通过神经网络实现。为了简化符号，定义为DecoderNetworkθ(·)，其中\(\theta\)表示网络参数。解码器的工作是，接收潜在变量z，并生成一张图像\(f_{\theta}(z)\)：

\[f_{\theta}(z) = \text{DecoderNetwork}_{\theta}(z).\tag{1.28}\]

分布\(p_{\theta}(x|z)\)可以定义为 \[p_{\theta}(x|z) = N(x\ |\ f_{\theta}(z), \sigma_{dec}^2 I), \quad\quad 对于某些超参数\sigma_{dec}. \tag{1.29}\]

\(p_{\theta}(x|z)\)的解释是，我们通过网络估计 \(f_{\theta}(z)\)，将其作为高斯的均值。若，我们从\(p_{\theta}(x|z)\)中抽取样本x，那么，通过再参数化技巧，我们可以将生成的图像\(\hat{x}\)写为 \[\hat{x} = f_{\theta}(z) + \sigma_{dec}\epsilon,\quad\quad \epsilon\sim N(0,I).\]

此外，如果我们取对数似然，可以证明

\begin{align} log\ p_{\theta}(x|z) &= log\ N(x|f_{\theta}(z), \sigma_{dec}^2 I)\\ &= log\ \frac{1}{\sqrt{(2\pi\sigma_{dec}^2)^d}}\text{exp}\ \Big\{-\frac{||x - f_{\theta}(z)||^2}{2\sigma_{dec}^2}\Big\}\\ &= -\frac{||x-f_{\theta}(z)||^2}{2\sigma_{dec}2} - \underbrace{log\ \sqrt{(2\pi\sigma_{dec}^2)^d}}_{\text{与}\theta\text{无关，可以忽略}} . \tag{1.30} \end{align}

回到ELBO，我们想要计算\(E_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z)]\)。如果我们直接计算期望值，我们需要计算一个积分

\begin{align} E_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z)] &= \int log\ [N(x|f_{\theta}(z), \sigma_{dec}^2 I)]\cdot N(z|\mu_{\phi}(x), \sigma_{\phi}^2(x))dz\\ &= -\int \frac{||x-f_{\theta}(z)||^2}{2\sigma_{dec}^2}\cdot N(z|\mu_{\phi}(x), \sigma_{\phi}^2(x)) dz + C, \end{align}

其中从高斯对数中得出的常数C可以被丢弃。通过再参数化技巧，我们将z写为\(z=\mu_{\phi}(x)+ \sigma_{\phi}(x)\epsilon\)，并将其代入上述方程。得到

\begin{align} E_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z)] &= -\int \frac{||x-f_{\theta}(z)||^2}{2\sigma_{dec}^2}\cdot N(z|\mu_{\phi}(x), \sigma_{\phi}^2(x)) dz\\ &\approx -\frac{1}{M}\sum_{m=1}^M\frac{||x - f_{\theta}(z^{(m)})||^2}{2\sigma_{dec}^2}\\ &= -\frac{1}{M}\sum_{m=1}^M\frac{||x- f_{\theta}(\mu_{\theta}(x) + \sigma_{\phi}(x)\epsilon^{(m)})||^2}{2\sigma_{dec}^2}.\tag{1.31} \end{align}

上述近似值是由于蒙特卡洛，其中随机性基于\(\epsilon\sim N(\epsilon|0, I)\)的采样。指数M指定了我们想要用来近似期望的蒙特卡洛样本的数量。请注意，输入图像x是固定的，因为\(E_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z)]\)是x的函数。

\(E_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z)]\)相对于\(\theta\)的梯度相对容易计算。由于仅\(f_{\theta}\)依赖于\(theta\)，我们可以进行自动微分。相对于\(\phi\)的梯度稍微困难，但它仍然是可计算的，因为我们使用链式法则并进入\(\mu_{\phi}(x)\)和\(\phi_{\phi}(x)\)。

检查方程（1.31），我们注意到一件有趣的事情，损失函数就是重建图像\(f_{\theta}(z)\)和真实图像x之间的ℓ2范数。这意味着，如果我们有生成的图像\(f_{\theta}(z)\)，我们可以通过通常的ℓ2损失直接与真实图像进行比较，如图1.6所示。

VAE训练 给定一个干净图像的训练数据集 \(\mathcal{X} = \{(x^{(l)})\}_{l=1}^L\)，VAE的训练目标是最大化ELBO

\[\stackrel{\huge argmax}{\theta,\phi}\sum_{x\in \mathcal{X}}\ ELBO_{\phi,\theta}(x),\]

其中，求和是对整个训练数据集。单一ELBO基于上述我们推导的各项和

\[ELBO_{\phi,\theta}(x) = E_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z) - D_{KL}(q_{\phi}(z|x) || p(z)). \tag{1.32}\]

这里，重建项是：

\[E_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z) \approx -\frac{1}{M}\sum_{m=1}^M\frac{||x - f_{\theta}(\mu_{\phi}(x) + \sigma_{\phi}(x)\epsilon^{(m)})||^2}{2\sigma_{dec}^2}, \tag{1.33}\]

而先验匹配项是

\[D_{KL}(q_{\phi}(z|x) || p(z)) = \frac{1}{2}(\sigma_{\phi}^2(x)d -d + ||\mu_{\phi}(x)||^2 - 2log\ \sigma_{\phi}(x)).\tag{1.34}\]

为优化\(\theta\)和\(\phi\)，我们可以运行梯度下降。梯度可以根据神经网络的张量图来获取。在计算机上，这是通过自动微分自动完成的。

让我们总结一下这些。

定理 1.4 （VAE训练）。为了训练VAE，我们需要解决优化问题 \[\stackrel{\huge argmax}{\theta,\phi}\sum_{x\in\mathcal{X}}\ ELBO_{\phi,\theta}(x),\]

其中

\begin{align} ELBO_{\phi,\theta}(x) = -\frac{1}{M}\sum_{m=1}^M\frac{||x-f_{\theta}(u_{\phi}(x) + \sigma_{\phi}(x)\epsilon^{(m)})||^2}{2\sigma_{dec}^2} + \\ \frac{1}{2}(\sigma_{\phi}^2(x)d - d + ||\mu_{\phi}(x)||^2 - 2dlog\ \sigma_{\phi}(x)). \tag{1.35} \end{align}

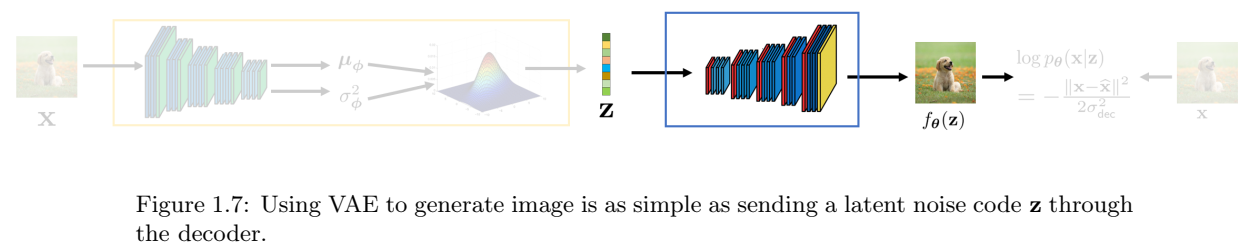
VAE推理。VAE的推理相对简单。一旦VAE被训练，我们可以丢掉编码器，并仅保留解码器，如图1.7所示。为了从模型中生成新的图像，我们选择随机潜在变量\(z\in R^d\)。通过将此z传递到解码器\(f_{\theta}\)，我们将能够生成新的图像\(\hat{x} = f_{\theta}(z)\)。