AEP 的结果：数据压缩

设\(X_1,X_2,\dots,X_n\)是抽取在概率质量函数p(x)的独立同分布随机变量。我们希望找到这种随机变量序列的短描述。我们将\(\mathcal{X}^n\)中的全部序列分为两个集合：典型集\(A_{\epsilon}^{(n)}\)及其补，如图3.1所示。

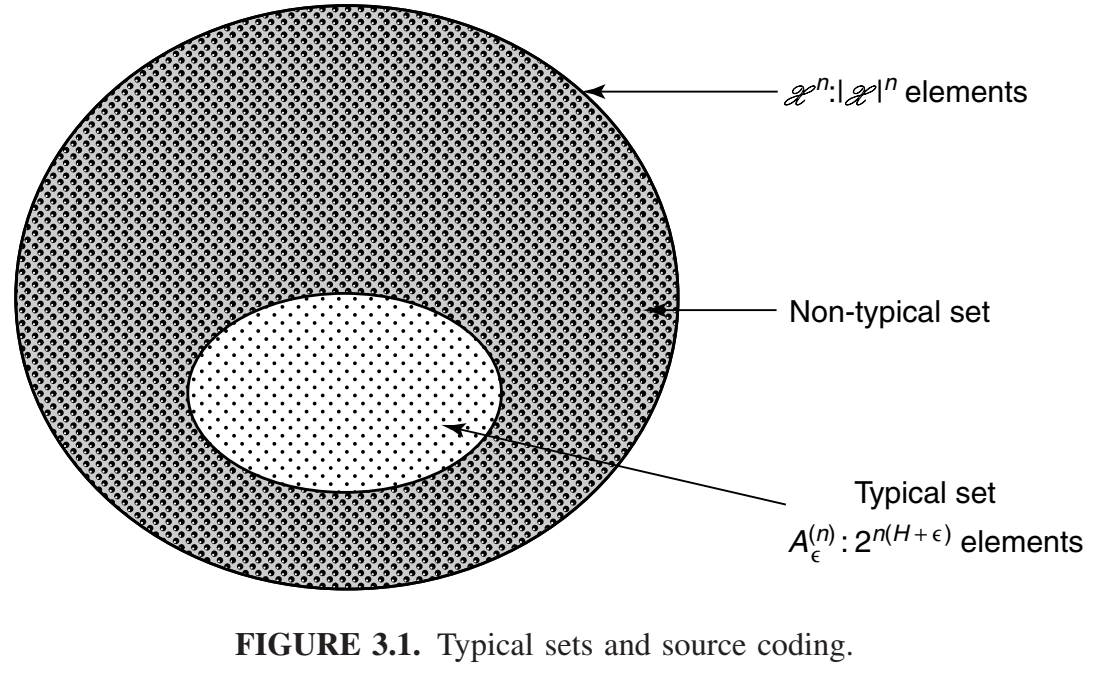
我们按照某种顺序（例如，字典顺序）对每个集合中的所有元素进行排序。然后，我们可以通过给出序列在集合中的索引来表示\(A_{\epsilon}^{(n)}\)中的每个序列。由于\(A_{\epsilon}^{(n)}\) 中有\(\le 2^{n(H+\epsilon}\)个序列，因此索引所需的比特位不超过 \(n(H + \epsilon) +1\ bits\) 。[可能需要额外的比特位，因为\(n(H + \epsilon)\)可能不是整数。] 我们在所有这些序列的前缀中添加一个 0，使得\(A_{\epsilon}^{(n)}\)中的每个序列的总长度不超过\(n(H + \epsilon) +2\ bits\) （参见图 3.2）。类似地，我们可以使用不超过\(n\ \text{log}\ |\mathcal{X}|+1\)比特位来索引不在\(A_{\epsilon}^{(n)}\)中的每个序列。在这些索引前面加上 1，我们就得到了\(\mathcal{X}^n\)中所有序列的编码。

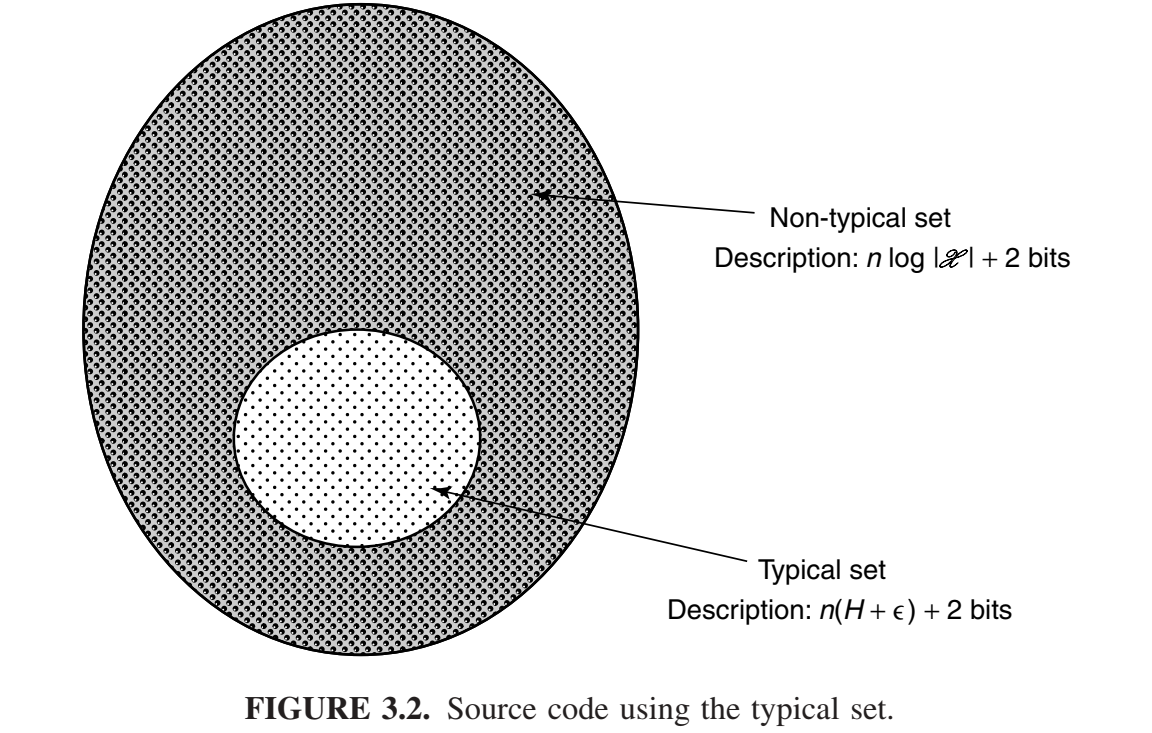
请注意上述编码方案的以下特点：

• 编码是一对一的，且容易解码。初始比特作为旗帜比特，来指示后面的码字的长度。
• 我们暴力枚举非典型集\(A_{\epsilon}^{(n)^c}\)，没有考虑\(A_{\epsilon}^{(n)^c}\)中元素数量少于\(\mathcal{X}^n\)中元素数量的事实。惊奇的是，这足以产生一个有效的描述。
• 典型序列有长度\(\approx nH\)的短描述。

我们使用符号\(x^n\)表示序列\(x_1,x_2,\dots,x_n\)。设\(l(x^n)\)为相应\(x^n\)的码字长度。若n足够大，使得\(Pr\{A_{\epsilon}^{(n)}\} 1-\epsilon\)，码字的期望长度为

\begin{align} E(l(X^n)) &= \sum_{x^n}p(x^x)l(x^n)\tag{3.17}\\ &= \sum_{x^n \in A_{\epsilon}^{(n)}}p(x^n)l(x^n) + \sum_{x^n \in A_{\epsilon}^{(n)^c}}p(x^n)l(x^n)\tag{3.18}\\ &\le \sum_{x^n \in A_{\epsilon}^{(n)}} p(x^n)(n(H + \epsilon) + 2)\\ &\quad + \sum_{x^n\in A_{\epsilon}^{(n)^c}}p(x^n)(n \text{log}|\mathcal{X}| + 2) \tag{3.19}\\ & = Pr\{A_{\epsilon}^{(n)}\} (n(H + \epsilon) + 2) + Pr\big\{A_{\epsilon}^{(n)^c}\big\}(n\text{log}|\mathcal{X}| + 2) \tag{3.20}\\ &\le n(H + \epsilon) + \epsilon n(\text{log}|\mathcal{X}|) + 2\tag{3.21}\\ &= n(H + \epsilon’), \tag{3.22} \end{align}

其中，\(\epsilon’ = \epsilon + \epsilon\ \text{log}\ |\mathcal{X}| + \frac{2}{n}\)可以任意小，通过适当选择\(\epsilon\)和n。因此，我们已经证明如下定理。

定理 3.2.1 设\(X^n\)为服从p(x)的i.i.d。\(\epsilon \gt 0\)。那么存在一个编码，将长度为n的序列\(x^n\)映射到二进制字符串，使得该映射是一对一（因此可逆），且

\[E\Big[\frac{1}{n}l(X^n)\Big] \le H(X) + \epsilon \tag{3.23}\]

对于足够大的n。

因此， 我们可以使用平均\(nH(X)\)比特来表示序列\(X^n\)。