熵和互信息之间的关系
我们可以将互信息\(I(X;Y)\)的定义重写为
\begin{align} I(X;Y) &= \sum_{x,y}p(x,y)\ \text{log}\ \frac{p(x,y)}{p(x)p(y)} \tag{2.35}\\ &= \sum_{x,y}p(x,y)\ \text{log}\frac{p(x|y)}{p(x)}\tag{2.36}\\ &= -\sum_{x,y}p(x,y)\ \text{log}\ p(x) + \sum_{x,y}\ p(x,y)\ \text{log}\ p(x|y)\tag{2.37}\\ &= -\sum_{x,y}p(x)\ \text{log}\ p(x) - \big(-\sum_{x,y}p(x,y)\ \text{log}\ p(x|y)\big)\tag{2.38}\\ &= H(X) - H(X|Y). \tag{2.39} \end{align}
因此,互信息 I (X; Y) 是由于了解 Y 而导致的 X 的不确定性的减少。
根据对称性,也可以得出 \[I(X;Y) = H(Y) - H(Y|X)/ \tag{2.40}\]
因此,X对Y的描述与Y对X的描述一样多。
由于\(H(X,Y) = H(X) + H(Y|X)\),如第2.2节所示,我们有
\[I(X;Y) = H(X) + H(Y) - H(X,Y). \tag{2.41}\]
最后,我们注意到 \[I(X;X) = H(X) - H(X|X) = H(X). \tag{2.42}\]
因此,随机变量与其自身的互信息就是该随机变量的熵。这就是熵有时被称为自信息的原因。
综合这些结果,我们得到以下定理。
定理 2.4.1 (互信息和熵) \[I(X;Y) = H(X) - H(X|Y) \tag{2.43}\]
\[I(X;Y) = H(Y) - H(Y|X)\tag{2.44}\]
\[I(X;Y) = H(X) + H(Y) - H(X,Y)\tag{2.45}\]
\[I(X;Y) = I(Y;X)\tag{2.46}\]
\[I(X;X) = H(X). \tag{2.47}\]
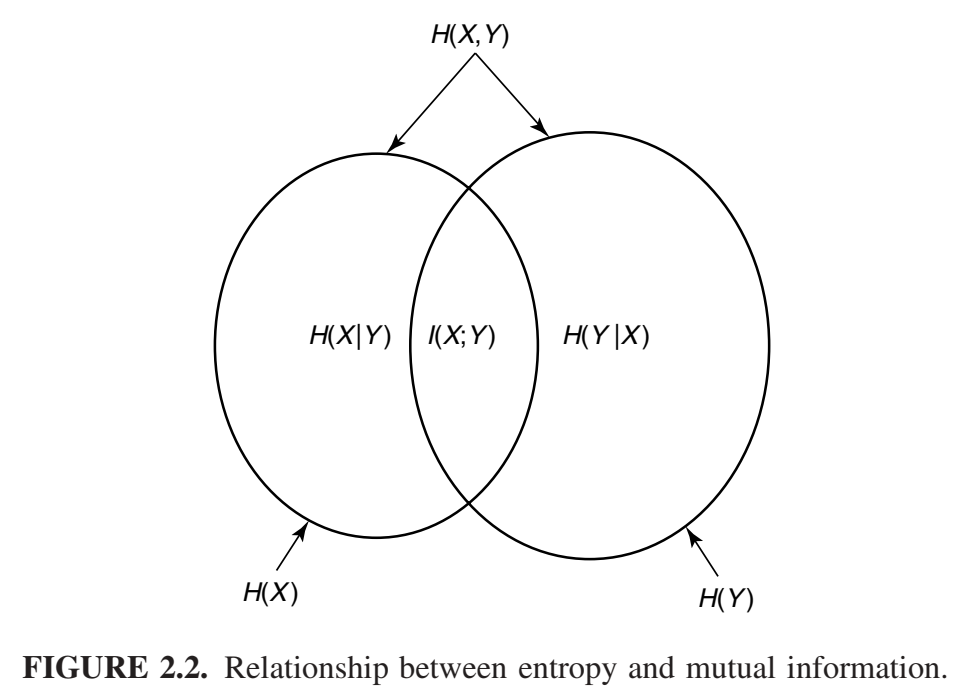
H(X)、H(Y)、H(X, Y)、H(X|Y)、H(Y|X) 和 I(X; Y) 之间的关系可以用韦恩图表示(图 2.2)。注意,互信息 I(X; Y) 对应于 X 中的信息与 Y 中信息的交集。
示例 2.4.1 对于示例2.2.1中的联合分布,很容易计算互信息\(I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) = 0.375\ bit\)。