Jensen不等式及其影响

在本节中，我们将证明前面定义的一些简单性质。我们从凸函数的性质开始。

定义 函数\(f(x)\)在区间 \((a,b)\) 上是凸函数，如果对于每个 \(x_1, x_2 \in (a, b)\) 且 \(0 \le \lambda \le 1\)，

\[f(\lambda x_1 + (1-\lambda)x_2) \le \lambda f(x_1) + (1-\lambda)f(x_2).\tag{2.72}\]

如果仅当λ= 0 或λ= 1 时等式成立，则函数 f 被称为严格凸函数。

定义 如果 −f 是凸函数，则函数 f 是凹函数。如果函数始终位于任意弦的下方，则函数是凸函数。如果函数始终位于任意弦的上方，则函数是凹函数。

凸函数的例子包括\(x^2\)、\(|x|\)，\(e^x\)，\(x\ \text{log}\ x\)(对于\(x \ge 0)\)等等。凹函数的例子包括\(\text{log}\ x)\)和\(\sqrt{x}\)，对于\(x \ge 0\)。图2.3展示了一些凸函数和凹函数的例子。请注意，线性函数\(ax +b\)既是凸也是凹的。凸性是信息论量（如熵和互信息）的许多基本性质的基础。在证明这些性质之前，我们先推导凸函数的一些简单结果。

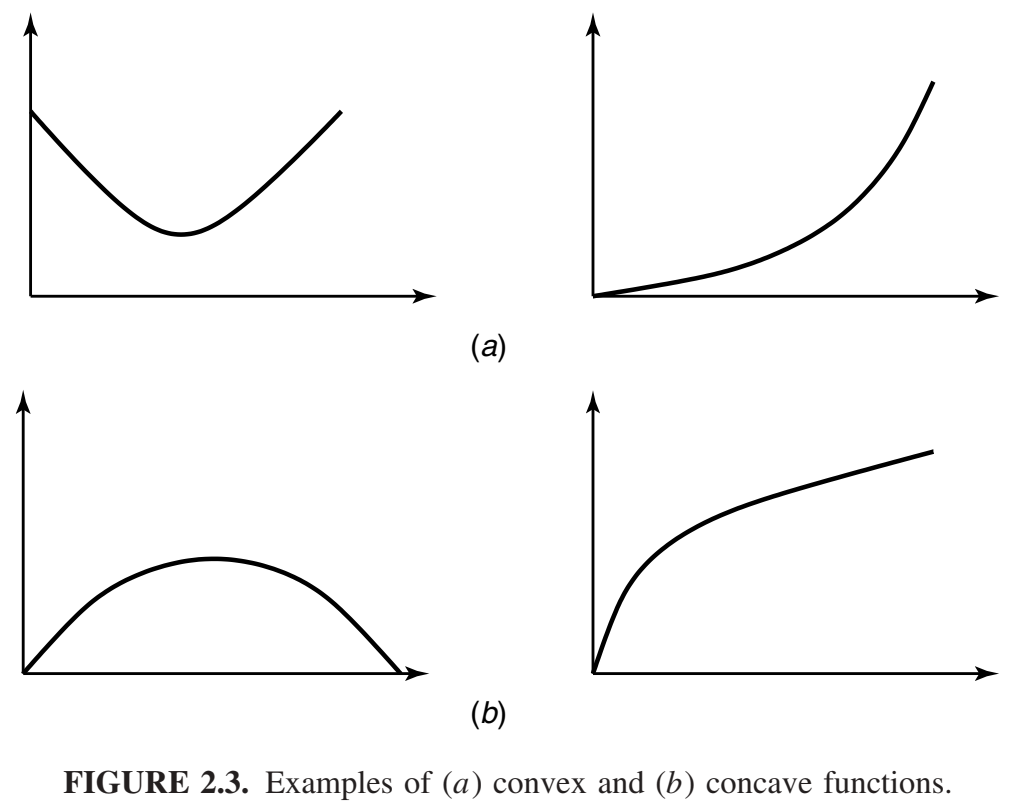
定理 2.6.1 如果函数 f 的二阶导数在某个区间上为非负（正），则该函数在该区间上是凸的（严格凸的）。

证明： 我们使用函数在\(x_0\)附近的泰勒级数展开 \[f(x) = f(x_0) + f’(x_0)(x-x_0) + \frac{f’’(x^{\star})}{2}(x-x_0)^2, \tag{2.73}\]

其中，\(x^{\star}\)在 \(x_0\)和x之间。通过假设，\(f’’(x^{\star}) \ge 0\)，所以，对于全部x，最后一项是非负的。

我们设\(x_0 = \lambda x_1 + (1-\lambda)x_2\)并取 \(x = x_1\)，得到 \[f(x_1) \ge f(x_0) + f’(x_0)((1-\lambda)(x_1-x_2)).\tag{2.74}\]

类似的，取\(x=x_2\)，得到 \[f(x_2) \ge f(x_0) + f’(x_0)(\lambda(x_2 - x_1)).\tag{2.75}\]

(2.74)乘以\(\lambda\)，(2.75)乘以\(1- \lambda\)，并相加，我的得到(2.72)。严格凸性的证明过程与此相同。

定理 2.6.1 可以让我们立即验证当 x ≥ 0 时 x²、ex 和 x log x 的严格凸性，以及当 x ≥ 0 时 log x 和 \(\sqrt{x}\) 的严格凹性。

令 E 表示期望。因此，在离散情况下，\(EX = \sum_{x\in\mathcal{X}}p(x)x\)；在连续情况下，\(EX = \int\ xf(x)dx\)。

下一个不等式是数学中最广泛使用的不等式之一，也是信息论中许多基本结果的基础。

定理 2.6.2 （Jensen不等式）如果f是凸函数，且X是随机变量， \[Ef(X) \ge f(EX). \tag{2.76}\]

此外，如果 f 是严格凸的，则 (2.76) 中的等式意味着 X = EX 的概率为 1（即 X 为常数）。

证明：我们通过对质点数量的归纳，证明了离散分布的这一结论。当 f 为严格凸函数时，等式成立的条件留给读者自行证明。

对于双质点分布，不等式变为

\[p_1f(x_1) + p_2f(x_2) \ge f(p_1x_1 + p_2x_2), \tag{2.77}\]

这直接来自凸函数的定义。假设该定理对于具有 k − 1 个质点的分布成立。则对于\(i = 1,2,\dots, k-1\)，记 \({p_i}′ = p_i/(1 − p_k)\)，得到

\begin{align} \sum_{i=1}^k p_if(x_i) &= p_k f(x_k) + (1-p_k)\sum_{i=1}^{k-1}p_i’f(x_i)\tag{2.78}\\ &\ge p_kf(x_k) + (1-p_k)f(\sum_{i=1}^{k-1}p_i’x_i)\tag{2.79}\\ &\ge f(p_kx_k + (1-p_k)\sum_{i=1}^{k-1}p_i’x_i)\tag{2.80}\\ &=f(\sum_{i=1}^k p_ix_i),\tag{2.81} \end{align}

其中第一个不等式来自归纳假设，第二个不等式来自凸性的定义。

该证明可以通过连续性参数扩展到连续分布。

我们现在用这些结果来证明熵和相对熵的一些性质。以下定理具有根本重要性。

定理 2.6.3 （信息不等式）设\(p(x), q(x), x\in\mathcal{X}\)为两个概率质量函数。那么 \[D(p||q) \ge 0\tag{2.81}\]

当且仅当\(p(x)=q(x)\)时，对于所有x，等号成立。

证明：设 \(A = \{x: p(x)\gt 0\}\)为p(x)的支持集。那么

\begin{align} -D(p||q) &= -\sum_{x\in A}p(x)\ \text{log}\frac{p(x)}{q(x)}\tag{2.83}\\ &= \sum_{x\in A}p(x)\ \text{log}\frac{q(x)}{p(x)}\tag{2.84}\\ &\le \text{log}\sum_{x\in A}p(x)\frac{q(x)}{p(x)}\tag{2.85}\\ &= \text{log}\sum_{x\in A}q(x) \tag{2.86}\\ &\le \text{log}\sum_{x\in \mathcal{X}}q(x) \tag{2.87}\\ &= \text{log}\ 1\tag{2.88}\\ &= 0, \tag{2.89} \end{align}

其中，（2.85）来自Jensen不等式。由于\(\text{log}\ t\)是t的严格凹函数，当且仅当\(q(x)/p(x)\)处处常量时【即，对于所有x，\(q(x) = cp(x)\)】，（2.85）中等号成立。因此，\(sum_{x\in A}q(x) = c\sum_{x\in A}p(x) = c\)。当且仅当\(\sum_{x\in A}q(x) = \sum_{x\in \mathcal{X}}q(x)= 1\)时，（2.87）中等号成立，意味着c=1。因此，当且仅当\(p(x) = q(x)\)时，对于全部x，得到\(D(p||q) = 0\)。

引理 （互信息的非负性）对于任意两个随机变量X，Y，

\[I(X;Y) \ge 0, \tag{2.90}\]

当且仅当X和Y独立时，等号成立。

证明：\(I(X;Y) = D(p(x,y)||p(x)p(y)) \ge 0\)，当且仅当\(p(x,y) = p(x)p(y)\)（即X、Y独立）时，等号成立。

引理
\[D(p(y|x)||q(y|x))\ge 0, \tag{2.91}\]

当且仅当对于所有 y 和 x，p(y|x) = q(y|x) 且满足 p(x) > 0 时，等号成立。

引理 \[I(X;Y|Z) \ge 0, \tag{2.92}\]

当且仅当，给定Z，X和Y条件独立时，等号成立。

我们现在证明，在范围 X 上的均匀分布是该范围的最大熵分布。由此可见，任何在该范围内的随机变量的熵都不大于 log |X|。

定理 2.6.4 \(H(X) \le \text{log}\ |\mathcal{X}|\)，其中\(|\mathcal{X}|\)表示范围X内的元素数量，当且仅当X是\(\mathcal{X}\)上的均匀分布时，等号成立。

证明：设\(u(x) = \frac{1}{\mathcal{X}}\)为\(\mathcal{X}\)上的均匀概率质量函数，且p(x)为x的概率质量函数。那么

\[D(p || u) = \sum\ p(x)\text{log}\frac{p(x)}{u(x)} = \text{log}|\mathcal{X}| - H(X).\tag{2.93}\]

因此，由于相对熵的非负性，

\[0 \le D(p||u) = \text{log} |\mathcal{X}| - H(X). \tag{2.94}\]

定理 2.6.5 （条件作用会降低熵）（信息不会造成伤害）

\[H(X|Y) \le H(X)\tag{2.95}\]

当且仅当X和Y独立时，等号成立。

证明： \(0\le I(X;Y) = H(X) - H(X|Y).\)

直观地说，该定理表明，知道另一个随机变量 Y 只能减少 X 的不确定性。请注意，这仅在平均水平上成立。具体来说，\(H(X|Y\ =\ y)\)可能大于或小于或等于 H(X)，但平均而言，\(H(X|Y) = \sum_y p(y)H(X|Y=y) \le H(X)\)。例如，在法庭案件中，具体的新证据可能会增加不确定性，但平均而言，证据会减少不确定性。

示例 2.6.1 设(X,Y)有以下联合分布：

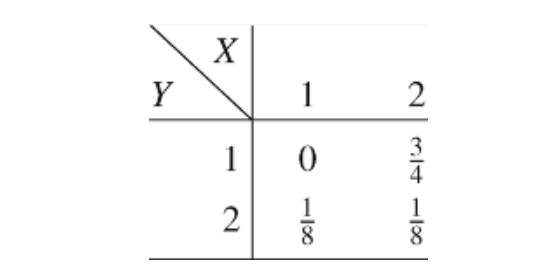
那么 \(H(X) = H(\frac{1}{8}, \frac{7}{8}) = 0.544\ bit\)， \(H(X|Y=1) = \ 0\ bits\)，以及 \(H(X|Y=2)=1\ bit\)。我们计算 \(H(X|Y) = \frac{3}{4}H(X|Y = 1) + \frac{1}{4}H(X|Y=2)= 0.25\ bit\)。因此，当Y=2被观测到时，X的不确定性增加，Y=1被观测到时，X的不确定性减少，但平均不确定性减少。

定理 2.6.6 （熵的独立性界限）设\(X_1,X_2,\dots,X_n\)根据\p((x_1,x_2,\dots,x_n)\)抽取。那么

\[H(X_1,X_2,\dots,X_n) \le \sum_{i=1}^n H(X_i) \tag{2.96}\]

当且就能当\(X_i\)独立时，等号成立。

证明： 通过熵的链式法则，

\begin{align} H(X_1,X_2,\dots,X_n) &= \sum_{i=1}^n H(X_i|X_{i-1},\dots,X_1) \tag{2.97}\\ &\le \sum_{i=1}^n H(X_i), \tag{2.98} \end{align}

其中不等式直接来自定理2.6.5.当且仅当对于所有i，\(X_i\)独立于\(X_{i-1},\dots,X_1\)时（即，当且仅当\(X_i\)独立），等号成立。