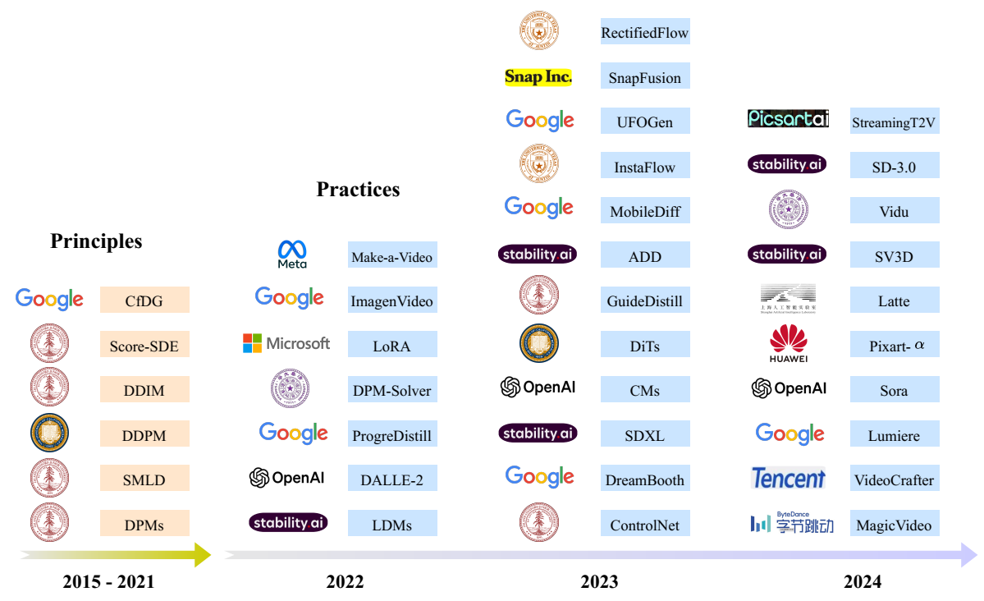
主要扩散模型及其相关类别
1.基于分数匹配的扩散模型 ● 噪声条件评分网络 (NCSN): 这是一种早期的基于分数匹配的扩散模型,它使用神经网络来学习数据分布的评分函数。 ● 潜空间评分生成模型 (LSGM): LSGM 使用变分自编码器 (VAE) 将数据压缩到潜空间,然后在潜空间中应用评分匹配来学习数据分布。 ● 基于分数的随机微分方程 (Score-SDE): Score-SDE 使用随机微分方程 (SDE) 来描述扩散过程,并使用神经网络来学习 SDE 的漂移项,该漂移项与数据分布的评分函数相关。 ● ScoreFlow: ScoreFlow 通过最大化似然函数的上界来训练基于分数的扩散模型。 2.潜变量模型 ● 潜扩散模型 (LDM): LDM 使用预训练的 VAE 将图像压缩到潜空间,然后在潜空间中应用扩散模型来生成图像。这种方法可以提高训练和推理效率,并生成更高质量的图像。 3.条件引导的扩散模型 ● 引导扩散 (GLIDE): GLIDE 使用分类器引导来控制扩散模型的生成过程,使其生成符合特定条件的图像。 ● 分类器引导扩散 (CfDG): CfDG...
关于 CNF 中时间依赖微分同胚映射的理解
在连续归一化流 (CNF) 中,时间依赖微分同胚映射是将简单分布(如标准正态分布)转化为复杂数据分布的关键机制。它通过一个随时间变化的向量场 vt(x)v_t(x)vt(x) 来实现,这个向量场决定了概率密度函数从初始分布 pθ(x)p_\theta(x)pθ(x) 到目标分布 p1(x)p_1(x)p1(x) 的演化过程。这个演化过程可以通过一个微分同胚映射 ϕt\phi_tϕt 来描述,它将时间 ttt 的概率密度函数 pt(x)p_t(x)pt(x) “推” 向时间 t+dtt+dtt+dt 的概率密度函数 pt+dt(x)p_{t+dt}(x)pt+dt(x)。 微分同胚映射的定义 微分同胚映射 ϕt\phi_tϕt 拥有以下性质: 双射: ϕt\phi_tϕt 是一个一一映射,也就是说,对于每一个 x,都有唯一一个 y 与之对应,反之亦然。 可微: ϕt\phi_tϕt 和它的逆映射 ϕt−1\phi_t^{−1}ϕt−1 都是可微的,这意味着它们是光滑且连续的。 保向: ϕt\phi_tϕt...
对连续性方程的深入解读
连续性方程本质上是一个描述守恒量的方程。在流匹配的语境下,这个守恒量就是概率密度。 概率密度的守恒 想象一下液体在管道中流动。如果液体不可压缩,那么无论管道粗细如何变化,单位时间内流过任何一个截面的液体总量都应该保持不变。这就是质量守恒定律的体现。 概率密度也遵循类似的守恒原则。假设我们有一个概率密度函数 pt(x)p_t(x)pt(x),它描述了在时间 ttt 时,随机变量 XXX 取值 xxx 的概率密度。随着时间的推移,pt(x)p_t(x)pt(x) 的形状可能会发生变化,但它所代表的总概率必须保持为 1。 连续性方程正是用来描述概率密度这种守恒特性的数学工具。 连续性方程的数学表达 连续性方程的表达式如下: ddtpt(x)+div(pt(x)vt(x))=0\frac{d}{dt} p_t(x) + div(p_t(x)v_t(x)) = 0 dtdpt(x)+div(pt(x)vt(x))=0 ddtpt(x)\frac{d}{dt} p_t(x)dtdpt(x) 表示概率密度函数 pt(x)p_t(x)pt(x)...
连续性方程在流匹配中的理解
连续性方程是偏微分方程 (PDE),它提供了一个必要且充分的条件,以确保向量场 vtv_tvt 生成概率路径 ptptpt。 换句话说,它验证了给定的向量场是否确实生成了期望的概率密度演变。 连续性方程: ddtpt(x)+div(pt(x)vt(x))=0\frac{d}{dt} p_t(x) + div(p_t(x)v_t(x)) = 0 dtdpt(x)+div(pt(x)vt(x))=0 其中: pt(x)p_t(x)pt(x) 是时间 ttt 的概率密度函数。 vt(x)v_t(x)vt(x) 是时间 ttt 的向量场。 divdivdiv 是关于空间变量 x=(x1,...,xd)x = (x^1, ..., x^d)x=(x1,...,xd) 的散度算子,即 div=∑i=1d∂∂xidiv = \sum_{i=1}^d \frac{\partial}{\partial x^i}div=∑i=1d∂xi∂ 。 连续性方程在流匹配中的作用: 验证向量场: 连续性方程用于检验学习到的 CNF 模型的向量场 vtv_tvt...
流匹配 (Flow Matching) 简介
流匹配 (FM) 是一种用于训练连续归一化流 (CNF) 的新方法,它能够以空前的规模训练 CNF。它基于一种称为“条件概率路径”的概念,该路径描述了从噪声样本到数据样本的转换过程。FM 的目标是通过回归固定条件概率路径的向量场来匹配该目标概率路径,而无需进行昂贵的模拟。 条件流匹配 (CFM) 为了使 FM 更加易于处理,引入了条件流匹配 (CFM) 的概念。CFM 避免了对难以处理的积分的依赖,并使用每个样本定义的概率路径和向量场。 CFM 目标函数: 1LCFM(θ) = Et,q(x1),p(x0) ||| vt(ψt(x0)) - d/dt ψt(x0) |||² 其中: θ 是 CNF 向量场的可学习参数。 t ∼ U(均匀分布)。 x1 是服从未知数据分布 q(x1) 的随机变量。 x0 ∼ p(x0) 是服从简单分布的随机变量,例如标准正态分布。 ψt 是与条件概率路径 pt(x|x1) 对应的流映射。 vt 是 CNF 向量场。 CFM 的优势: 与原始 FM...
计算CNF模型概率的方法
连续归一化流 (CNF) 模型通过一个时间依赖的微分同胚映射将简单分布(如标准正态分布)转化为复杂数据分布。要计算 CNF 模型在任意数据点 x1x_1x1 的概率,我们需要利用连续性方程和流的轨迹方程。 连续性方程和概率密度的变化 连续性方程描述了概率密度的守恒特性: ddtpt(x)+div(pt(x)vt(x))=0\frac{d}{dt}p_t(x) + div(p_t(x)v_t(x)) = 0 dtdpt(x)+div(pt(x)vt(x))=0 其中: pt(x)p_t(x)pt(x) 是时间 t 的概率密度函数。 vt(x)v_t(x)vt(x) 是时间 t 的向量场,由 CNF 模型学习得到。 divdivdiv 是散度算子。 这个方程表明,概率密度的变化率必须与其“流动”情况相互抵消,以保证总概率守恒。 计算概率密度的步骤 步骤 1: 瞬时变量的变化 将连续性方程与流的轨迹方程 (ddtϕt(x)=vt(ϕt(x))\frac{d}{dt}\phi_t(x) =...